 | ÁREA: LOGICA | GRADO: 9° |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 5 Y 6 DE JUNIO DEL 2025 | PERIODO: PRIMERO | |
VALOR: SENTIDO DE PERTENENCIA | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 5 Y 6 DE JUNIO DEL 2025
GRADO: 9°
TEMA: REGLA DE TRES
SUBTEMA: REGLA DE TRES SIMPLE
LOGRO. Aplica la regla de tres para desarrollar situaciones de problemas cotidianos.
NOTA: CONTINUIDAD CLASE ANTERIOR
Existen dos tipos de regla de tres simple, lo cual dependerá de acuerdo a la relación que tengan las magnitudes que intervengan en el problema.
Regla de Tres Simple Directa:
La regla de tres simple directa resulta de comparar dos magnitudes directamente proporcionales, por lo tanto el producto en aspa de sus valores son iguales.
Ejemplo:
Si 40 obreros hacen 100 m. de carretera por día, cuántos metros por día harán 70 obreros.
Solución:
A más obreros obviamente se harán más metros de carretera, entonces son magnitudes directamente proporcionales:
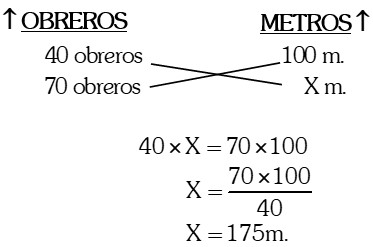
Regla de Tres Simple Inversa:
Resulta de comparar dos magnitudes inversamente proporcionales, por lo tanto, el producto en línea de sus valores son iguales.
Ejemplo:
Si 45 obreros pueden hacer un edificio en 20 días; en cuánto tiempo harán 60 obreros la misma obra.
Solución:
A más obreros se terminará en menos tiempo la obra; entonces son magnitudes inversamente proporcionales:
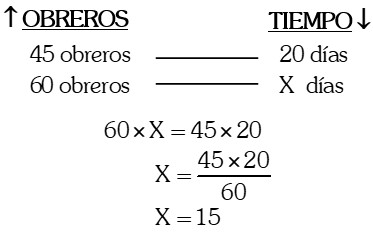
Regla de Tres Compuesta
Resulta de comparar más de dos magnitudes directamente proporcionales ó inversamente proporcionales.
Método de las Rayas
Las magnitudes que participan se clasifican en tres grupos perfectamente definidos:
1.- Causa:
Son aquellas magnitudes que permiten la realización de la obra y están conformadas por las condiciones que se tienen para ejecutarla, asi por ejemplo:
- Obreros
- Rendimiento
- Capital (económico)
- Animales
- Habilidad
- Capacidad
- Máquinas
- Esfuerzo
- etc.
2.- Tiempo:
Son aquellas magnitudes de tiempo en la que se realiza la obra:
- Meses
- Años
- Días
- Horas por día
- Raciones diarias de comida
3.- Efecto:
Son aquellas magnitudes que representan a la obra en sí y los inconvenientes que estas tienen para ser realizadas:
- Las medidas de la obra (largo, ancho, alto, profundidad, espesor, área, volumen, etc.)
- Dificultad de la obra.
- Resistencia del medio.
Aplicación del Método:
Se igualan los dos productos que resultan de multiplicar todos los valores que siguen a una misma raya.
Ejemplo:
Sabiendo que 20 obreros, trabajando 6 horas diarias pueden hacer una obra en 10 días; determinar en cuántos días, 30 obreros doblemente hábiles, trabajando 8 horas diarias pueden hacer una obra cuya dificultad es dos veces la anterior.
Solución: extraemos los datos y los separamos en grupos de causa; tiempo y efecto:
Luego, multiplicamos todos los valores que encontremos al seguir una raya y lo igualamos al resultado de la multiplicación de todos los valores que se encuentren al seguir otra de las rayas; así:
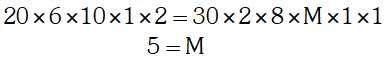
ACTIVIDAD EN CASA:
REALIZA LOS SIGUIENTES EJERCICIOS
1. Dos ruedas están unidas por una correa transmisora. La primera tiene un radio de 
cm y la segunda de 
cm. Cuando la primera ha dado 
vueltas, ¿cuántas vueltas habrá dado la segunda?
2. La escala en un mapa es la siguiente: 
cm en el mapa representan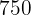 
m en la realidad. ¿A cuánto metros en la realidad equivalen 
cm en el mapa?
3. Seis personas pueden vivir en un hotel durante 
días por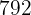 
€. ¿Cuánto costará el hotel de 
personas durante ocho días?
4. Una tienda de conveniencia cobra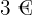 
por cada 
enviados, y si la cantidad no es exacta, se cobra la cantidad correspondiente. Si una persona depositó 
, ¿cuánto le cobró la tienda de conveniencia por el envío?
5. Si con botes de 
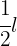de pintura cada uno se han pintado 
m de verja de 
cm de altura. Calcular cuántos botes de 
de pintura serán necesarios para pintar una verja similar de 
cm de altura y 
metros de longitud.
del polinomio por el valor del enunciado. Por lo tanto, en este caso debemos sustituir la letra 
para 
![\begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-926a3afab513e8e260f70cdff6067cb3_l3.svg "Rendered by QuickLaTeX.com")
para 
![\begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://www.polinomios.org/wp-content/ql-cache/quicklatex.com-084cbb91ab71bd12b7ab283e3207289e_l3.svg "Rendered by QuickLaTeX.com")
