Ciencia Exactas: CLASE DE MATEMATICA GRADO 11° DEL 13 DE AGOSTO DEL 2025 TEMA: LIMITE DE UNA FUNCION

	ÁREA: MATEMATICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 13 DE AGOSTO DEL 2025	PERIODO: TERCERO
	VALOR: RESPONSABILIDAD	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 13 DE AGOSTO DEL 2025

GRADO: 11°

TEMA: LIMITE DE UNA FUNCION

SUBTEMA: LIMITE DE UNA FUNCION

LOGRO. Reconoce el limite de una función.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Que es limite?. lluvia de ideas

LIMITE DE UNA FUNCION:

¿Qué es el límite de una función?

En matemáticas, el límite de una función en un punto es el valor al cual se aproxima la función cuando x se acerca a ese punto.

El límite de la función f(x) en el punto x=a se representa utilizando la siguiente notación:

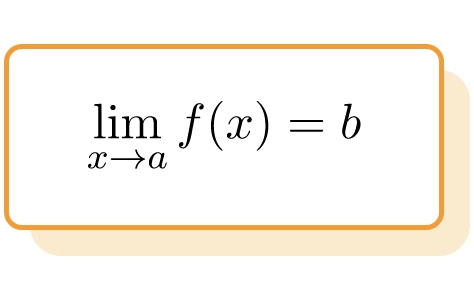
La expresión anterior significa que el límite de la función f(x) cuando x tiende a $a$ es igual a b.

Para acabar de entender qué significa el límite de una función, vamos a hallar el siguiente límite:

$\displaystyle\lim_{x\to 2}(x^2-4x+5)= \ \color{red}\bm{?}$

Para ver a qué valor se aproxima la función cuando x tiende a 2, podemos ir calculando imágenes de la función de puntos cada vez más cerca de x=2:

Como puedes ver en las dos tablas anteriores, a medida que vamos tomando valores más próximos a x=2, la función se va acercando a 1. Por lo tanto, el límite de la función cuando x tiende a 2 es 1.

$\displaystyle\lim_{x\to 2}(x^2-4x+5)= \color{red}\bm{1}$

A continuación puedes ver la función representada gráficamente. Como puedes comprobar, la función se acerca a 1 cuando x se aproxima a 2.

Fíjate en la gráfica que la función se acerca al mismo valor independientemente de si nos acercamos por la izquierda o por la derecha. Más abajo profundizaremos más sobre este concepto de los límites.

Cómo calcular el límite de una función:

Para calcular el límite de una función en un punto simplemente tenemos que sustituir el valor de ese punto en la función.

Por ejemplo, si queremos resolver el límite cuando x tiende a 3 de la siguiente función, debemos sustituir las x de la función por 3:

$\begin{array}{l}\displaystyle\lim_{x \to \color{blue}\bm{3}\color{black}} \left(x^2+5x-7\right)=\\[3ex]=\color{blue}\bm{3}\color{black}^2+5\cdot \color{blue}\bm{3}\color{black}-7=\\[3ex]=9+15-7=17\end{array}$