Ciencia Exactas: CLASE DE MATEMATICA GRADO 6° DEL 5 DE SEPT DEL 2025 TEMA: CLASIFICACION DE LOS NUMEROS RACIONALES

	ÁREA: MATEMATICA	GRADO: 6°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 5 DE SEPT DEL 2025	PERIODO: TERCER
	VALOR: LA AMISTAD	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALORES, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION"

FECHA: DEL 5 DE SEPTIEMBRE DEL 2025

GRADO: 6°

TEMA: LOS NUMEROS RACIONALES

SUBTEMA: REPRESENTACION DE NUMEROS RACIONALES EN FORMA DE FRACCION EN LA RECTA NUMERICA

LOGRO. Realiza operaciones con los números racionales.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿que es un racional?. lluvia de ideas.

PAGINA 25 volumen 2

REPRESENTACION DE NUMEROS RACIONALES EN FORMA DE FRACCION EN LA RECTA NUMERICA

1- Representación de números racionales en la recta numérica

Para representar los números racionales en la recta numérica, tienes que comparar los números dados, para lo cual deberás transformar de número decimal a fracción o de fracción a número decimal.

1.1- Representación de números decimales en la recta numérica

Si tienes que transformar las fracciones a número decimal, puedes ubicar los números racionales en la recta numérica de la siguiente forma; si son números negativos y positivos dibuja una recta dividida en 2 mitades simétricas desde el origen, es decir, desde el número 0. A la izquierda del número 0 ubicas los números negativos y a la derecha los números positivos, de menor a mayor, manteniendo la misma distancia entre dos números consecutivos. Para ubicar los décimos se divide la distancia entre dos números consecutivos en 10 partes iguales. Los números decimales inexactos los puedes aproximar para que sea más fácil ubicarlos.

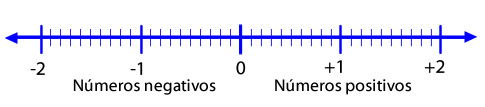
recta_numeros_racionales_0.jpg (485×107)

Una vez que ubiques todos los decimales en la recta numérica, puedes anotar los números racionales originales.

Recuerda que, los números positivos mientras más cerca del cero menor será su valor y los números negativos mientras más cerca del cero mayor será su valor.

Ejemplo: Representa los siguientes números racionales en la recta numérica;

recta_numeros_racionales_1.jpg (493×56)

- Primero debes transformar las fracciones a números decimales y el número mixto a fracción impropia y luego a número decimal.

recta_numeros_racionales_2.jpg (506×385)

Recuerda: Para transformar un número mixto a fracción impropia debes multiplicar el entero por el denominador y sumar el numerador, este resultado se escribe en el numerador y el denominador se mantiene igual.

Ejemplo:

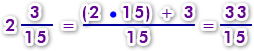
recta_numeros_racionales_3.jpg (254×51)

- Entonces los números que tienes que representar son los siguientes;

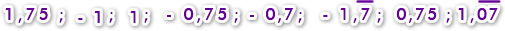
recta_numeros_racionales_4.jpg (505×31)

- Aproxima los números decimales inexactos, los que tienen centésimos también los puedes aproximar. En este caso no aproximaremos, ya que, sabemos que (0,05) se ubica en la mitad entre dos décimos de la recta que dibujaremos.

recta_numeros_racionales_5.jpg (558×143)

Nota: Si necesitas ubicar los centésimos con exactitud, solo tienes que dividir la distancia entre 2 décimos en 10 partes iguales.

- Ahora puedes comparar y ubicar los números decimales en la recta numérica.

recta_numeros_racionales_6.jpg (508×93)

- Anota los números racionales originales en la recta numérica.

recta_numeros_racionales_7.jpg (495×116)

1.2- Representación fracciones en la recta numérica

Si tienes que transformar los números decimales a fracción, puedes ubicar los números racionales en la recta numérica de la siguiente forma; divide en segmentos iguales los trazos unitarios de la recta numérica según lo que indica el denominador, y la fracción se ubica tantos lugares, a la derecha o a la izquierda según el signo de la facción, como indica el numerador. Como serán varias fracciones puedes igualar sus denominadores y luego ubicarlos en la recta numérica o bien dividir los tramos en forma independiente para cada fracción dentro de la misma recta numérica.

Cuando hay una fracción impropia para ubicarla en la recta numérica es necesario transformarla en número mixto.

Ejemplo: Representa los siguientes números racionales en la recta numérica;

recta_numeros_racionales_8.jpg (505×51)

- Primero debes transformar los números decimales a fracción, como ayuda primero enumera con letras los números racionales para que no te confundas e identifica cuales son decimales finitos, decimales infinitos periódicos y decimales infinitos semiperiódicos.

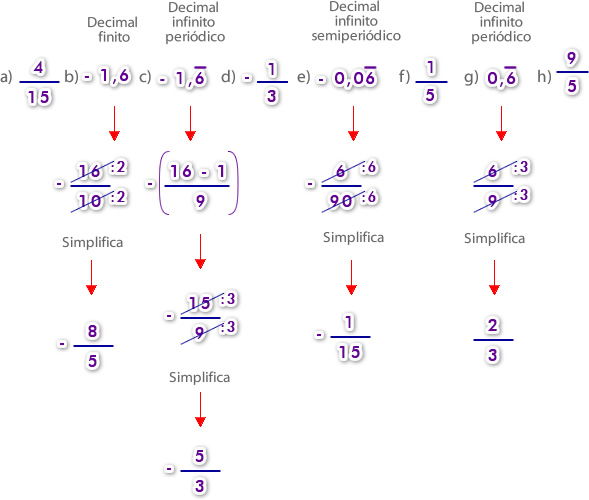
recta_numeros_racionales_9.jpg (589×500)

- Ahora como ya transformaste todos los decimales a fracción, para ubicarlas en la recta numérica, como son varias fracciones, iguala sus denominadores sacando el mínimo común múltiplo.