CLASE DE MATEMATICA GRADO 9° DEL 11 DE AGOSTO DEL 2025 SEMANA TEMA: SISTEMA DE ECUACIONES LINEALES 2X2

 

	ÁREA:  MATEMATICA	GRADO: 9°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL  11  DE  AGOSTO  DEL 2025	PERIODO: TERCERO
	VALOR: RESPONSABILIDAD	FRASE:  “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

 

FECHA: DEL  11 DE  AGOSTO  DEL 2025

 GRADO: 9°

TEMA:  SISTEMA DE ECUACIONES LINEALES 2X2

SUBTEMA:  SOLUCION POR EL METODO GRAFICO

LOGRO. Reconoce  los diferentes sistemas de ecuaciones.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿ Que es un sistema de ecuaciones?

DEFINICION PAGINA   150

SISTEMA DE ECUACIONES LINEALES

SOLUCION POR METODO GRAFICO

¿Qué es el método gráfico?

El método de gráfico es un método utilizado para resolver sistemas de ecuaciones. Concretamente, el método gráfico consiste en representar las ecuaciones del sistema en una gráfica y ver en qué punto se cortan (en el siguiente apartado veremos exactamente cómo se hace).

Existen más métodos para resolver sistemas de ecuaciones, como por ejemplo el método de sustitución, el método de reducción, o método de igualación. Si estás más interesad@ en estos otros métodos, puedes buscar la explicación de cada uno de ellos en esta web.

Cómo resolver un sistema de ecuaciones por el método gráfico

Para resolver un sistema de ecuaciones por el método gráfico se deben hacer los siguientes pasos:

1. Despejar la incógnita y de las dos ecuaciones del sistema.

2. Construir una tabla de valores para cada ecuación.

3. Representar gráficamente las dos ecuaciones en el plano cartesiano. Se obtendrán dos rectas:

a.) Si las dos rectas se cortan en un punto, dicho punto de corte es la solución del sistema de ecuaciones (Sistema Compatible Determinado).

b.)Si las dos rectas se superponen, el sistema de ecuaciones tiene infinitas soluciones (Sistema Compatible Indeterminado).

c.) Si las dos rectas son paralelas (no se cortan), el sistema de ecuaciones no tiene solución (Sistema Incompatible).

El método gráfico es difícil de entender, por eso a continuación hemos resuelto paso a paso un sistema de ecuaciones lineales por el método gráfico para que veas cómo se aplica este procedimiento.

Ejemplo de un sistema de ecuaciones resuelto por el método gráfico

Vista la teoría sobre el método gráfico, vamos a explicar paso a paso la resolución de un sistema de ecuaciones utilizando el método gráfico a modo de ejemplo:

En primer lugar, tenemos que despejar la incógnita y de las dos ecuaciones que forman el sistema:

Una vez tenemos despejada la y de ambas ecuaciones, debemos hacer una tabla de valores para cada ecuación. Y para construir una tabla de valores simplemente tenemos que otorgar valores (los que quieras) a la incógnita x, hacer los cálculos que se indican en cada ecuación, y el valor obtenido será la coordenada y correspondiente a ese punto.

Entonces, creamos la tabla de valores para la primera ecuación:

• 

• 

Una vez hemos calculado la tabla de valores de una ecuación, debemos representar los puntos obtenidos en un gráfico. Recuerda que la primera coordenada de un punto, la coordenada x, corresponde al eje horizontal, y la segunda coordenada de un punto, la coordenada y, corresponde al eje vertical.

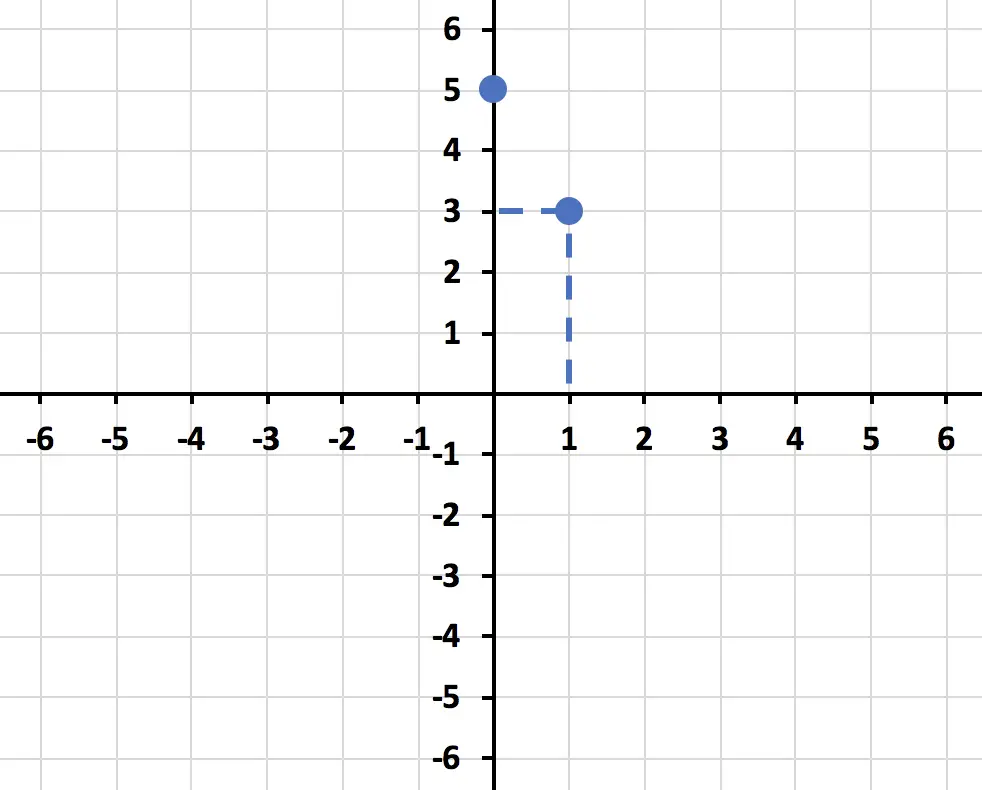
Y unimos los puntos representados para formar una recta:

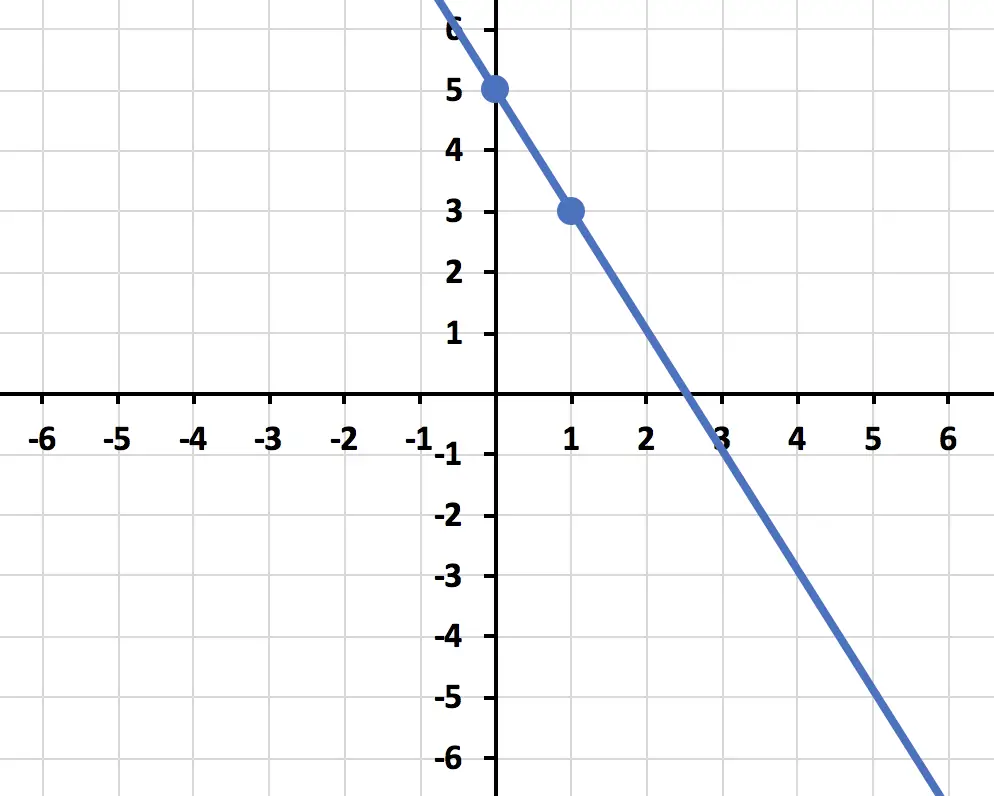
Aunque calculando dos puntos por cada ecuación es suficiente, si quieres puedes calcular algún otro punto para comprobar que la recta está bien representada.

Ahora debemos repetir el mismo proceso con la otra ecuación del sistema. Así pues, construimos la tabla de valores de la segunda ecuación:

• 

• 

Cuando ya tenemos la tabla de valores, representamos los puntos obtenidos en el mismo gráfico que hemos representado la recta anterior:

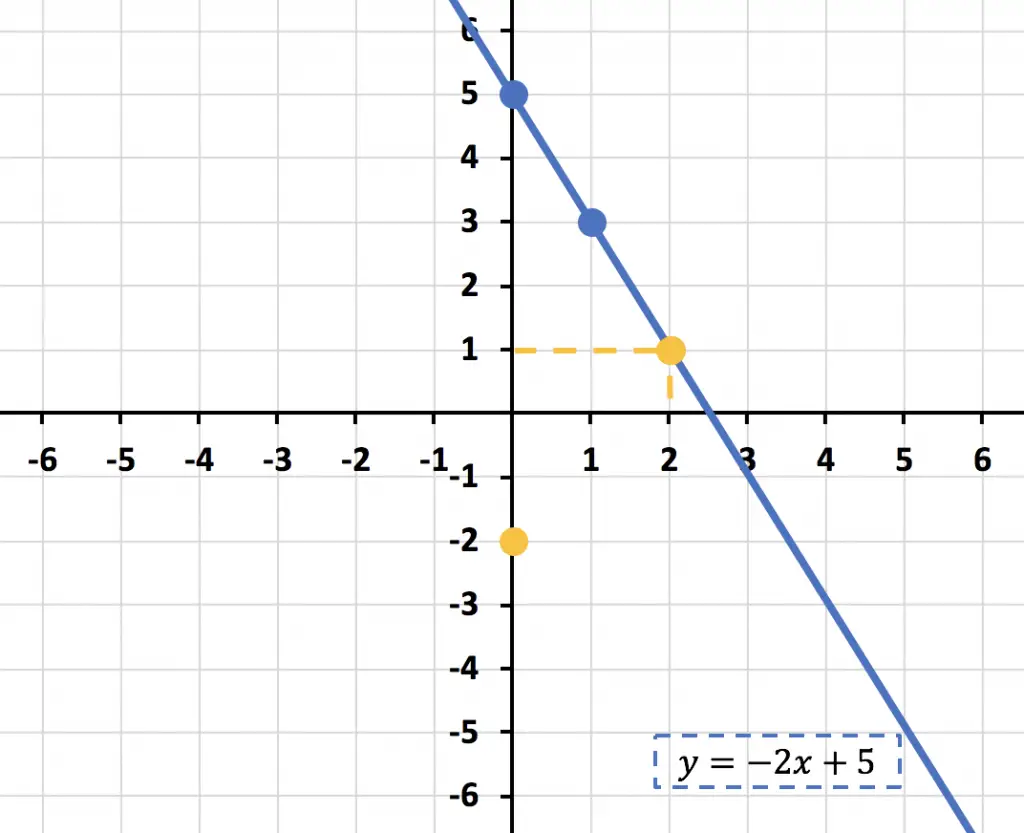
Y unimos los puntos para formar la otra recta:

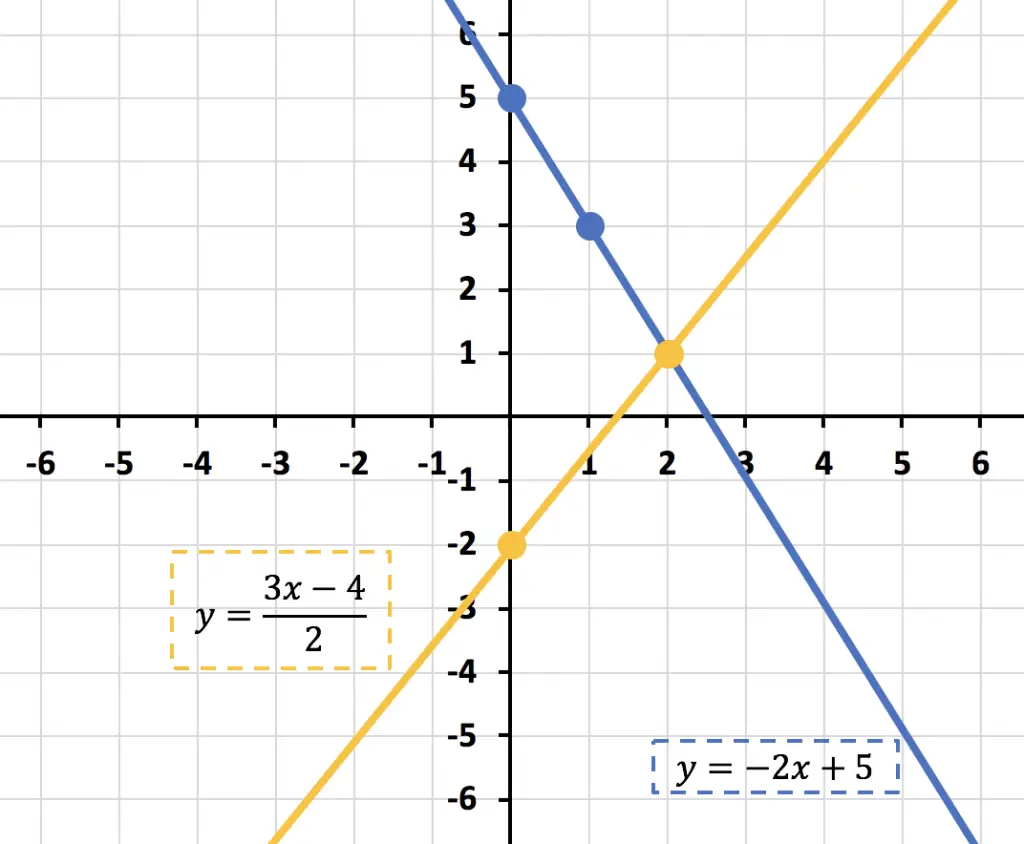
Una vez hemos representado las dos ecuaciones en un gráfico, ya podemos saber cuál es la solución del sistema de ecuaciones. La solución del sistema de ecuaciones es el punto donde se cortan las dos rectas, que en este caso es el punto (2,1):

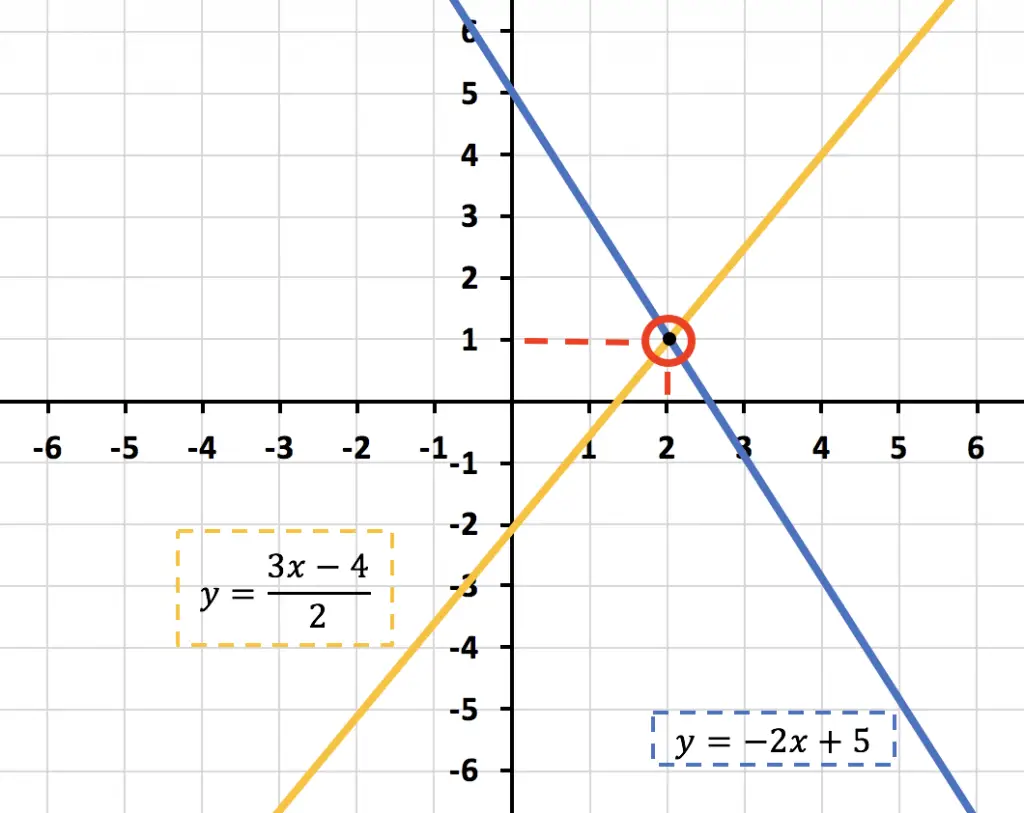
Como las rectas solamente se cruzan en el punto (2,1) la única solución del sistema de ecuaciones es:

En este caso, el sistema tiene una sola solución, por lo que se trata de un Sistema Compatible Determinado (SCD). Sin embargo, ten en cuenta que si las dos rectas estuvieran representadas una encima de la otra, el sistema tendría infinitas soluciones y por tanto sería un Sistema Compatible Indeterminado (SCI). Por otro lado, si las dos rectas fueran paralelas, el sistema no tendría ninguna solución y por tanto sería un Sistema Incompatible (SI).

ACTIVIDAD EN CASA:

Ejercicio 1

Resuelve el siguiente sistema de ecuaciones por el método gráfico:

Ejercicio 2

Resuelve el siguiente sistema de ecuaciones con fracciones por el método gráfico: