CLASE DE MATEMATICA GRADO 11° DEL 15 DE OCTUBRE DEL 2025 TEMA: CALCULO DE LIMITES

 

	ÁREA: MATEMATICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL  15  DE OCTUBRE DEL 2025	PERIODO: CUARTO
	VALOR: LA  AMISTAD	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

         

  

FECHA: DEL  15 DE OCTUBRE DEL 2025

 GRADO: 11°

TEMA: CALCULO DE LIMITES

SUBTEMA: LIMITES DE FUNCIONES INDETERMINADAS

LOGRO. Reconoce el limite de una función.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Que es limite?. lluvia de ideas

PAGINA 139 DEFINICION

CALCULO DE LIMITES DE FUNCIONES INDETERMINADAS:

Infinito entre infinito

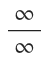
Dividir un número entre infinito es cero, pero si dividimos el propio infinito entre infinito ¿también es cero?

No, no tiene solución, por eso es indeterminado.

Indeterminación infinito entre infinito

La indeterminación infinito entre infinito suele producirse en límites al infinito de funciones con fracciones. Aunque la indeterminación sea el cociente de dos infinitos, el resultado no tiene por qué dar infinito.

Este tipo de forma indeterminada se resuelve por comparación. Es decir, se observa el grado del numerador y el grado del denominador y, según cuál sea mayor, el resultado del límite es uno u otro. Puedes ver todos los casos en el siguiente enlace:

Ejemplo 1:

El polinomio del numerador es de segundo grado, mientras que el del denominador es de tercer grado, por lo tanto, la solución del límite es 0.

Ejemplo 2:

Ejemplo 3:

En este caso, los dos polinomios son de segundo grado, por lo que tenemos que dividir los coeficientes de los términos de mayor grado para hallar el límite al infinito positivo.

Ejemplo 4:

Aunque el límite sea cuando x tiende a menos infinito, la indeterminación infinito entre infinito se resuelve de la misma manera.

Ejemplo de indeterminación del tipo ∞/∞

Tomemos la función g(x) = (3x^2 + 1)/(2x^2 – 1) cuando x tiende a infinito. Al evaluar el límite, obtenemos ∞/∞. Dividimos cada término por x^2 :

• lim (x → ∞)(3 + 1/x^2)/(2 – 1/x^2) = 3/2.

Ejemplo de indeterminación del tipo 0 × ∞

Para ilustrar la indeterminación del tipo 0 × ∞, consideramos la función h(x) = x*(sin(1/x)) cuando x tiende a 0. Aquí, tenemos 0*∞. Reescribimos h(x) como:

• h(x) = (sin(1/x))/1/x.

Usamos el límite y obtenemos:

• lim (x → 0) h(x) = 1.

Ejemplo de indeterminación del tipo ∞ – ∞

Considere la función k(x) = sqrt(x^2 + 1) – x cuando x tiende a infinito. Al evaluar el límite, obtenemos ∞ – ∞. Simplificamos:

• k(x) = (sqrt(x^2 + 1) – x)(sqrt(x^2 + 1) + x)/(sqrt(x^2 + 1) + x).

Al simplificar obtenemos:

• lim (x → ∞) k(x) = 1/ 2x = 0.

Ejemplo de indeterminación del tipo 1^∞

Para la indeterminación del tipo 1^∞, tomemos la función m(x) = (1 + 1/x)^x cuando x tiende a infinito. Se transforma usando logaritmos:

• ln(m(x)) = x*ln(1 + 1/x).

Aplicando L’Hôpital después de la forma 0*∞ se puede encontrar que lim (x → ∞) m(x) = e.

Ejemplo de indeterminación del tipo 0^0

Considere la función n(x) = (x^2)*(sin(1/x)) cuando x tiende a 0. Aquí, tenemos 0^0. Usando logaritmos, transformamos:

• ln(n(x)) = ln(x^2)*(sin(1/x)).

Ejemplo de indeterminación del tipo ∞^0

Finalmente, veamos la indeterminación del tipo ∞^0 con la función p(x) = x^(1/x). Donde, al calcular el límite cuando x tiende a infinito, usamos:

• ln(p(x)) = (1/x)*ln(x).

ACTIVIDAD EN CASA:

RESUELVE LOS SIGUIENTES EJERCICIOS

Ejercicio 1

Calcula el límite de la siguiente función racional:

 

Ejercicio 2

Resuelve el siguiente límite indeterminado:

Ejercicio 3

Resuelve el siguiente límite al infinito:

Ejercicio 4

Soluciona el siguiente límite indeterminado:

Ejercicio 5

Calcula el siguiente límite al menos infinito: