ÁREA: FISICA | GRADO: 11° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 13 DE MARZO DEL 2025 | PERIODO: PRIMERO | |
VALOR: SENTIDO DE PERTENENCIA | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 13 DE MARZO DEL 2025
GRADO: 11°
TEMA: MOVIMIENTO ARMONICO SIMPLE
SUBTEMA: DINAMICA DE UN M.A.S
LOGRO. Reconoce la física como el estudio de los fenómenos.
Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste.
Como la fuerza F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial Ep.
La expresión de la energía potencial es
Donde c es cualquier constante. Se toma como nivel cero de la energía potencial Ep=0 cuando el móvil está en el origen, x=0, por lo que c=0
La energía total E, es la suma de la energía cinética Ek y de la energía potencial Ep que es constante.
Ejercicios resueltos de movimiento armónico simple
Ejercicio 1
Un objeto describe un movimiento armónico simple cuya amplitud es de 0,5 m y su frecuencia de oscilación es de 2 Hz. En el instante inicial se encuentra en X = 0,5 m.
Escribir las ecuaciones de posición, velocidad y aceleración en función del tiempo.
Calcular la posición, la velocidad y la aceleración para t = 0,35 s.
Solución
Calculamos la velocidad angular mediante su fórmula, es decir como el producto del 2π por la frecuencia.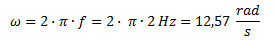
Determinamos el ángulo de fase. Dado que en el instante t = 0 el móvil se encuentra en el desplazamiento máximo positivo, podemos ver que no hay desplazamiento con respecto a una función coseno, es decir que la fase es de 0 radianes.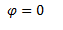
Planteamos las ecuaciones de posición, velocidad y aceleración. No hace falta indicar la fase dentro del argumento de la función ya que la misma es 0.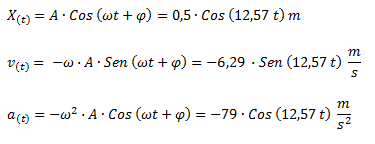
Calculamos la posición, la velocidad y la aceleración para t = 0,35 s.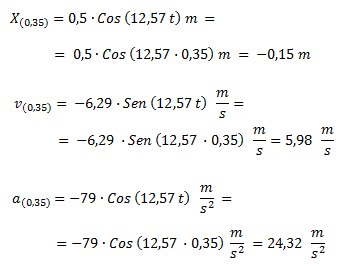
Ejercicio 2
Un oscilador armónico describe un movimiento según la siguiente función.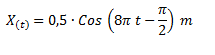
Indicar la velocidad angular, la frecuencia de oscilación, la velocidad máxima y la aceleración máxima.
Solución
La velocidad angular la obtenemos directamente de la expresión dada.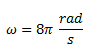
Despejamos la frecuencia de la fórmula de velocidad angular y reemplazamos los valores.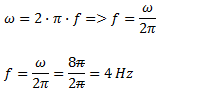
La velocidad máxima y la aceleración máxima se calculan con sus respectivas fórmulas. Recordemos que estas formulas son similares a las de velocidad y aceleración en función del tiempo, reemplazando por “1” a la función coseno (ya que ese el máximo valor que esa función puede alcanzar) y expresando el resultado en forma positiva.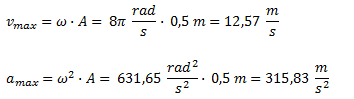
Ejercicio 3
Un oscilador armónico describe un movimiento según la siguiente expresión: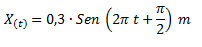
Expresar la posición mediante una función coseno positiva y escribir las ecuaciones de velocidad y aceleración en función del tiempo.
Solución
Para convertir una función seno positiva en una función coseno positiva debemos restarle a la fase 90° (es decir π/2), ya que la función coseno se encuentra adelantada 90° con respecto a la función seno. Debido a que la fase dada es π/2, la fase para la función coseno es 0.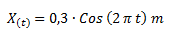
De la ecuación calculada, obtenemos la amplitud, la velocidad angular y la fase.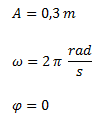
En base a los datos anteriores indicamos las ecuaciones de velocidad y aceleración en función del tiempo.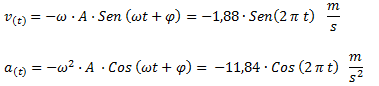
ACTIVIDAD EN CASA :
RESUELVE EL SIGUIENTES EJERCICIO DEL M.A.S
1. Un objeto describe un movimiento armónico simple cuya amplitud es de 0,15 m y su frecuencia de oscilación es de 5 Hz. En el instante inicial se encuentra en X = 0,10 m.
Escribir las ecuaciones de posición, velocidad y aceleración en función del tiempo.
Calcular la posición, la velocidad y la aceleración para t = 0,25 s.






No hay comentarios.:
Publicar un comentario