ÁREA: MATEMATICA | GRADO: 10° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 13 DE MARZO DEL 2025 | PERIODO: PRIMERO | |
VALOR: SENTIDO DE PERTENENCIA | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 13 DE MARZO DEL 2025
GRADO: 10°
TEMA: FUNCIONES
SUBTEMA: REPRESENTACION DE FUNCIONES
LOGRO. Reconoce el las funciones y su relación.
Representación verbal
En esta forma, se describe la relación funcional por medio de un texto con el suficiente nivel de detalle.
Ejemplos:
- “La estatura de una persona depende de su edad”
- “La población humana depende del tiempo”
- “El área de un rectángulo es base por altura”
Representación algebraica
En esta forma se expresa la función como una ecuación que relaciona la variable independiente y la variable dependiente. Para la variable independiente generalmente se usa la letra x, para la dependiente la letra y o el símbolo f(x). Esta forma es muy utilizada en Cálculo, junto con la representación gráfica.
Mediante una fórmula o ecuación definimos la regla que deben cumplir dos números para estar relacionados.
Ejemplos:
Una forma de interpretar el primer ejemplo es: dos números x e y están relacionados por la función si ocurre que Por ejemplo, los valores cumplen esto, por lo tanto, están relacionados. De la misma forma se pueden interpretar las demás expresiones.
Representación numérica
Esta también es llamada representación tabular. Se presenta una tabla donde figuran los valores de la variable independiente y a la par los valores correspondientes de variable dependiente. La tabla puede construirse de manera horizontal o vertical. Esta forma es generalmente utilizada para anotar los datos de un experimento en la vida real.
Ejemplo:
| x | y |
|---|---|
| -2 | -5 |
| -1 | -2 |
| 0 | 1 |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
Representación visual
La forma más utilizada de representación visual es la gráfica de una función, que consiste en los puntos del plano cartesiano cuyas coordenadas son las parejas de valores de entrada y salida de la función.
La gráfica es entonces el conjunto de puntos Sobre el eje horizontal (eje x) se sitúan los valores de la variable independiente y sobre el eje vertical (eje y) los valores correspondientes de la variable dependiente.
Ejemplos:
La gráfica de una función es una representación útil para saber su comportamiento. Si es un punto en la gráfica, entonces es la altura de la gráfica en el punto x. Esta puede ser positiva, negativa o cero, lo cual depende del signo de f(x). También el dominio y el rango pueden verse plasmados sobre los ejes.
ACTIVIDAD EN CASA:
REALIZA PAGINA 36



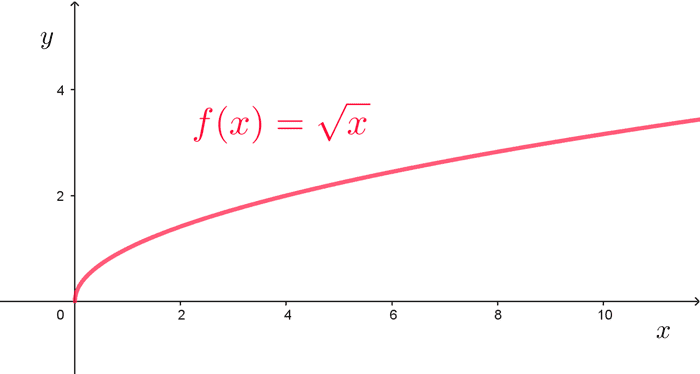
No hay comentarios.:
Publicar un comentario