CLASE DE FISICA GRADO 11° DEL 24 DE ABRIL DEL 2025 SEMANA TEMA: ENERGIA MECANICA DEL MAS - EJERCICIOS

 

	ÁREA: FISICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL  24 DE ABRIL DEL 2025	PERIODO: PRIMERO
	VALOR: SENTIDO DE PERTENENCIA	FRASE:  “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 24 DE ABRIL DEL 2025 

 GRADO: 11°

TEMA: ENERGIA MECANICA EN EL MAS

SUBTEMA: ENERGIA MECANICA EN EL MAS EJERCICIOS

LOGRO. Reconoce la física como el estudio de los fenómenos.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué es  la energía mecánica?. lluvia de ideas.

ENERGIA MECANICA EN EL MAS EJERCICIOS

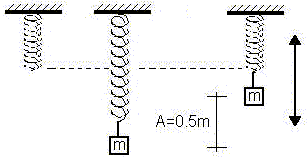
El período de una masa suspendida por un resorte es directamente proporcional al cuadrado de una masa. El período de una masa suspendida en un resorte es independiente a la longitud. El período de una masa suspendida en un resorte es inversamente proporcional a la Raíz cuadrada de K. Enunciado del ejercicio n° 1 Un cuerpo de 4 kg de masa está sujeto a un resorte helicoidal, y oscila verticalmente con movimiento armónico simple. La amplitud es de 0,5 m, y en el punto más alto del movimiento el resorte tiene su longitud natural. Calcúlese la energía potencial elástica del resorte, la energía cinética del cuerpo, su energía gravitacional respecto al punto más bajo del movimiento y la suma de estas tres energías, cuando el cuerpo está: a) En su punto más bajo. b) En su posición de equilibrio, y cuando está en su punto de equilibrio la energía Ep = 0, porque X = 0. c) En su punto más alto. Desarrollo Datos: m = 4 kg A = 0,5 m Fórmulas: k = F x Ep = ½·k·x² Solución k = 4 kg·9,8 m/s² 0,5 m k = 78,4 N/m Esquema de los resortes sometidos a carga suspendida a) Ep = ½·k·x² Ec = ½·m·v² = 0 Ep = ½·78,4·5² Ep = 9,8 J Ec = 0 (porque su velocidad es cero). Epg = m·g·h/2 = 0 (porque la altura es 0). ET = Ep + Ec + Epg = 9,8 N·m b) V = √k/m·√A² - x² V = 2,21 m/s Entonces: Ec = ½·4·2,21² Ec = 9,76 J Epg = ½·m·g·h Epg = ½·4·9,8·0,5 Epg = 9,8 J ET = Ep + Ec + Epg = 19,56 J c) Ep = ½·k·x² Ec = ½·m·v² = 0 Como es en este caso para el punto más alto se considera la energía como negativa, definida así por su amplitud (-A). Ep = ½·78,4·0,5² Ep = -9,8 J Epg = ½·m·g·h Epg = 4·9,8·½ Epg = 19,6 J ET = Ep + Ec + Epg = 9,8 N·m

ACTIVIDAD EN CASA:

RESUELVE.

1. Un cuerpo de 8 kg de masa está sujeto a un resorte helicoidal, y oscila verticalmente con movimiento armónico simple. La amplitud es de 0,15 m, y en el punto más alto del movimiento el resorte tiene su longitud natural. Calcúlese la energía potencial elástica del resorte, la energía cinética del cuerpo, su energía gravitacional respecto al punto más bajo del movimiento y la suma de estas tres energías, cuando el cuerpo está:

a) En su punto más bajo.

b) En su posición de equilibrio, y cuando está en su punto de equilibrio la energía E_p = 0, porque X = 0.

c) En su punto más alto.