ÁREA: MATEMATICA
GRADO: 9°
DOCENTE: ENAIDO MALDONADO POLO
CORREO: matematica. ceqa@gmail.com
FECHA: DEL 9 Y 10 DE JUNIO DEL 2025
PERIODO: TERCERO
VALOR: SENTIDO DE PERTENENCIA
FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”
| ÁREA: MATEMATICA | GRADO: 9° |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 9 Y 10 DE JUNIO DEL 2025 | PERIODO: TERCERO | |
VALOR: SENTIDO DE PERTENENCIA | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 9 Y 10 DE JUNIO DEL 2025
GRADO: 9°
TEMA: RACIONALIZACION Y NUMEROS COMPLEJOS
SUBTEMA: RACIONALIZACION Y NUMEROS COMPLEJOS
LOGRO. Reconoce e identifica la racionalización de los reales.
Racionalización del tipo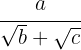 
Y en general cuando el denominador sea un binomio con al menos un radical.
Se multiplica el numerador y denominador por el conjugado del denominador.
El conjugado de un binomio es igual al binomio con el signo central cambiado:
También tenemos que tener en cuenta que: "suma por diferencia es igual a diferencia de cuadrados".
Ejemplos
1 Racionalizar la expresión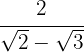 
Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
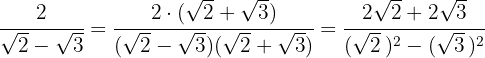
En el denominador extraemos los radicandos y dividimos por 
, es decir, cambiamos el numerador de signo
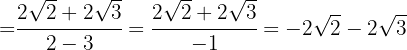
2 Racionalizar la expresión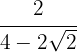 
Multiplicamos y dividimos la fracción por el conjugado del denominador
Efectuamos la suma por diferencia en el denominador, realizamos las operaciones y simplificamos la fracción dividiendo por 
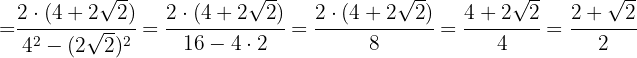
3 Racionalizar la expresión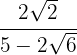 
Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados
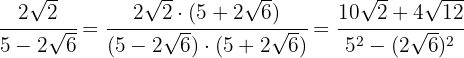
En el numerador descomponemos en factores al 
y extraemos factores, terminamos realizando las operaciones del denominador
Ejemplos de ejercicios de racionalización radicales
1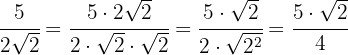 
2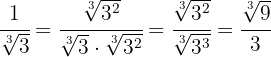 
3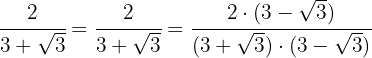 
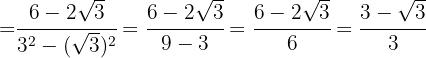
4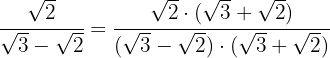 
5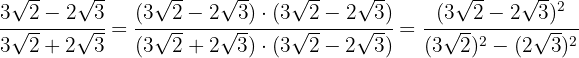 
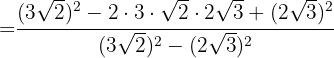
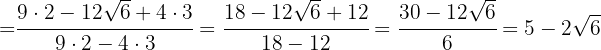
Podría decirte que el conjunto de los números complejos contiene a los números reales, se representan con el símbolo C y que incluyen las raíces de todos los polinomios, pero ¿qué quiere decir esto? ¿por qué necesitamos los números complejos?
Dicho con otras palabras lo anterior, recordamos que con los números reales no podemos resolver las raíces pares de números negativos:
Por tanto, necesitamos los números complejos para poder resolver con las raíces negativas de índice par.
Unidad imaginaria
Se le llama unidad imaginaria al número i, que es igual a la raíz de menos uno:
Con este número, ya podemos dar solución cuando tengamos raíces negativas:
Según las propiedades de las raíces, la raíz negativa podemos ponerla como esa misma raíz positiva, multiplicada por raíz de menos uno.
Finalmente, la raíz positiva ya tiene solución en el conjunto de los números reales y la raíz de menos uno la sustituimos por el número i.
Forma de los números complejos
Forma binómica
Un número complejo Z (no confundirse con C, que es el conjunto al que pertenecen) se puede representar de la forma:
Perteneciendo a y b al conjunto de los números reales.
Esta forma de escribir los números complejos corresponde a la forma binómica, que tiene dos partes:
- a = Parte real
- b = Parte imaginaria
Éstos son ejemplos de números complejos en forma binómica:
Si la parte real de un número complejo es 0, ese número es imaginario puro, ya que solo tiene parte imaginaria:
El número i es un número imaginario puro.
La forma binómica se utiliza en física a la hora de operar con vectores, donde la parte imaginaria se representa mediante la letra j, en vez de con la letra i.
Por otro lado, si no tiene parte imaginaria, estamos hablando de un número real puro, que no es ni más ni menos que un número real:
No hay comentarios.:
Publicar un comentario