ÁREA: EST Y LOG | GRADO: 8° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 28 DE JULIO DEL 2025 | PERIODO: TERCERO | |
VALOR: RESPONSABILIDAD | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 28 DE JULIO DEL 2025
GRADO: 8°
TEMA: MEDIDAS DE TENDECIA NO CENTRAL
SUBTEMA: MEDIDAS DE TENDENCIA CENTRAL
LOGRO. Reconoce las medidas de tendencia no central
ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Cuáles son los gráficos estadísticos?. lluvia de ideas.
MEDIDAS DE TENDENCIA NO CENTRAL
Cálculo de los Percentiles:
Existen varios métodos para el cálculo de percentiles. Veamos uno de los más sencillos (válido para datos no agrupados):
1. Agrupamos las muestras de menor a mayor valor
2. Calculamos la posición que ocupa el percentil buscado aplicando la siguiente fórmula:
siendo N el número total de muestras analizadas y la letra "i" el percentil buscado
3. Si el resultado anterior (x) no tiene decimales, el percentil se obtiene seleccionando el valor de la muestra que ocupa la posición x.
4. Si el resultado (x) tiene decimales, el percentil se obtiene haciendo la media de las muestras en posición x y x+1
EJEMPLO DE PERCENTIL
EJEMPLO Calcular el percentil 40 (P40) de las siguientes muestras de notas en matemáticas de un aula (notas de 0 a 20): 16, 10, 12, 8, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14- Ordenamos de menor a mayor: 1, 8, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20
- N = número de muestras = 15 muestras
- x = (N · i) / 100 = (15 · 40) / 100 = 6
- Como x = 6 es un número sin decimales, entonces el percentil 40 es el valor de la muestra que ocupa la posición 6
- P40 (percentil 40) = 10
ACTIVIDAD EN CASA:REA LIZA UN EJERCICIO DE PERCENTILE, DECILES Y CUARTILES
Existen varios métodos para el cálculo de percentiles. Veamos uno de los más sencillos (válido para datos no agrupados):
1. Agrupamos las muestras de menor a mayor valor
2. Calculamos la posición que ocupa el percentil buscado aplicando la siguiente fórmula:
siendo N el número total de muestras analizadas y la letra "i" el percentil buscado
3. Si el resultado anterior (x) no tiene decimales, el percentil se obtiene seleccionando el valor de la muestra que ocupa la posición x.
4. Si el resultado (x) tiene decimales, el percentil se obtiene haciendo la media de las muestras en posición x y x+1
- Ordenamos de menor a mayor: 1, 8, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20
- N = número de muestras = 15 muestras
- x = (N · i) / 100 = (15 · 40) / 100 = 6
- Como x = 6 es un número sin decimales, entonces el percentil 40 es el valor de la muestra que ocupa la posición 6
- P40 (percentil 40) = 10
LOGICA:TEMA: LOS PORCENTAJESSUBTEMA: LOS PORCENTAJESLOGRO. Reconoce el porcentaje de cualquier cantidadPROBLEMAS CON PORCENTAJES
Problemas resueltos de calcular porcentajes
Podemos calcular porcentajes de varias formas. Nosotros aplicamos una regla de tres simple. Recordad que, para ello, tenemos que identificar el total con el 100%. Más información en Calcular porcentajes (teoría y ejemplos).
Podemos calcular porcentajes de varias formas. Nosotros aplicamos una regla de tres simple. Recordad que, para ello, tenemos que identificar el total con el 100%. Más información en Calcular porcentajes (teoría y ejemplos).
Problema 1
Un concesionario tiene 120 coches, el 35% de ellos son blancos y el 5% rojos. ¿Cuántos coches de cada color hay?
SOLUCION
Tenemos que calcular el 35% y el 5% de 120.
Como el total de coches es 120, lo identificamos con el 100%.
Coches blancos:
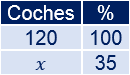
Aplicamos una regla de tres:
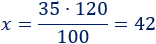
Coches rojos:
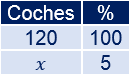
Aplicamos una regla de tres:
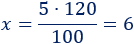
Por tanto, en el concesionario hay 42 coches blancos y 6 coches rojos.
Un concesionario tiene 120 coches, el 35% de ellos son blancos y el 5% rojos. ¿Cuántos coches de cada color hay?
SOLUCION
Tenemos que calcular el 35% y el 5% de 120.
Como el total de coches es 120, lo identificamos con el 100%.
Coches blancos:

Aplicamos una regla de tres:
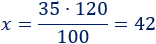
Coches rojos:

Aplicamos una regla de tres:
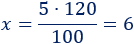
Por tanto, en el concesionario hay 42 coches blancos y 6 coches rojos.
Problema 2
En el colegio A, les gusta el rock a 12 de sus 60 alumnos. En el colegio B, les gusta el rock a 18 de sus 120 alumnos. ¿A qué porcentaje de alumnos les gusta el rock en cada colegio? ¿En qué colegio gusta más el rock?
SOLUCION
Calculamos el porcentaje de alumnos a los que les gusta el rock en cada colegio para poder comparar la proporción.
Colegio A:
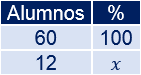
Aplicamos una regla de tres:
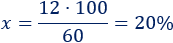
Colegio B:
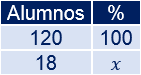
Aplicamos una regla de tres:
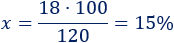
Tenemos
- En el colegio A, el rock gusta al 20% de los alumnos.
- En el colegio B, el rock gusta al 15% de los alumnos.
Por tanto, el rock gusta más en el colegio A.
Observad que la proporción es mayor en colegio A que en el colegio B, aunque el número de alumnos a los que les gusta el rock es mayor en el colegio B.
En el colegio A, les gusta el rock a 12 de sus 60 alumnos. En el colegio B, les gusta el rock a 18 de sus 120 alumnos. ¿A qué porcentaje de alumnos les gusta el rock en cada colegio? ¿En qué colegio gusta más el rock?
SOLUCION
Calculamos el porcentaje de alumnos a los que les gusta el rock en cada colegio para poder comparar la proporción.
Colegio A:

Aplicamos una regla de tres:
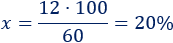
Colegio B:

Aplicamos una regla de tres:
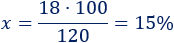
Tenemos
- En el colegio A, el rock gusta al 20% de los alumnos.
- En el colegio B, el rock gusta al 15% de los alumnos.
Por tanto, el rock gusta más en el colegio A.
Observad que la proporción es mayor en colegio A que en el colegio B, aunque el número de alumnos a los que les gusta el rock es mayor en el colegio B.
Problema 3
De los 684 lanzamientos que realizó Alberto, falló 513. ¿Qué porcentaje de lanzamientos fallidos tiene Alberto?
SOLUCION
Identificamos 684 con el 100%:

Aplicamos una regla de tres:
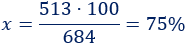
El porcentaje de lanzamientos fallidos de Alberto es el 75%.
ACTIVIDAD EN CASA:RESUELVE LOS SIGUIENTES EJERCICIOS
De los 684 lanzamientos que realizó Alberto, falló 513. ¿Qué porcentaje de lanzamientos fallidos tiene Alberto?
SOLUCION
Identificamos 684 con el 100%:

Aplicamos una regla de tres:
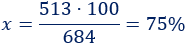
El porcentaje de lanzamientos fallidos de Alberto es el 75%.
Problema 1
Lara acertó el 85% de las preguntas del test de inglés. Si el test tenía un total de 160 preguntas, ¿en cuántas preguntas no acertó?
Problema 2
Problema 2


No hay comentarios.:
Publicar un comentario