CLASE DE MATEMATICA GRADO 6° DEL 29 DE JULIO DEL 2025 TEMA: PROPIEDADES DE LA POTENCIACION

 

	ÁREA: MATEMATICA	GRADO: 6°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 29 DE JULIO DEL 2025	PERIODO: TERCER
	VALOR: SENTIDO DE PERTENENCIA	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALORES, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION"

FECHA: DEL 29 DE JULIO DEL 2025

 GRADO: 6°

TEMA:  PROPIEDADES DE LA POTENCIACION

SUBTEMA: PROPIEDADES DE LA POTENCIACION

LOGRO. Reconoce las propiedades de la potenciación.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿que son los números enteros?. lluvia de ideas.

PROPIEDADES DE LA POTENCIACION

EJERCICIOS DE LAS PROPIEDADES DE LA POTENCIACION

PAGINA 160 EJEMPLOS

Tenemos tres tipos de ejercicios:

• Primero, calculamos potencias básicas.
• Después, calculamos potencias aplicando sus propiedades.
• Finalmente, simplificamos expresiones algebraicas con potencias, pudiendo haber parámetros.

Ejercicio 1 

Calcular las potencias:

• Dos elevado a cinco: $2^5$
• Cinco al cuadrado: $5^2$
• Dos al cubo: $2^3$

¿Por qué crees que se dice "al cuadrado" y "al cubo" para referirse a las potencias "elevado a 2" y "elevado a 3", respectivamente?

SOLUCION:

Dos elevado a cinco ($2^5$)

La base es 2 y el exponente es 5. Aplicamos la definición de potencia, es decir, multiplicamos la base, 2, por sí misma tantas veces como indica el exponente, 5:

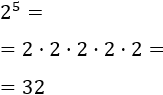
Cinco al cuadrado ($5^2$)

La base es 5 y el exponente es 2:

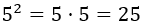
Dos al cubo ($2^3$)

La base es 2 y el exponente es 3:

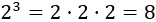
"Al cuadrado" y "al cubo":

• El área de un cuadrado de lado $L$ es $L\cdot L$, es decir, $L^2$, por eso la potencia "elevado a 2" se dice "al cuadrado". Por ejemplo, cuando calculamos $3^2$ estamos calculando el área del cuadrado de lado 3.
• El volumen de un cubo de lado $L$ es $L\cdot L\cdot L$, es decir, $L^3$, por eso la potencia "elevado a 3" se dice "al cubo".

Ejercicio 2 

Calcular las siguientes potencias:

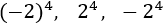
SOLUCION:

$(-2{)}^4$

La base es negativa, pero como el exponente es par, el resultado es positivo:

$2^4$

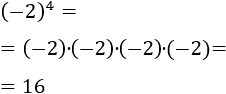
Como la base es positiva, el resultado es positivo:

$-2^4$

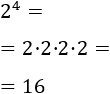
Como no hay paréntesis, el signo está fuera de la potencia, así que el resultado será negativo, aunque el exponente sea par:

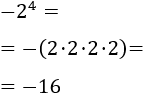
Ejercicio 3 

Calcular las siguientes potencias:

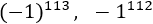
Las potencias de $-1$ son $1$ ó $-1$, dependiendo de la paridad del exponente. El resultado de la primera potencia es $-1$ porque el exponente es impar:

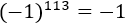
El resultado de la segunda potencia es $-1$ porque, aunque el exponente sea par, el signo negativo no está en la base, sino multiplicando la potencia:

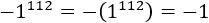
La base de la primera potencia es $-1$ y la de la segunda es $1$.

Ejercicio 4

Calcular el producto de potencias:

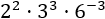
Las bases de las tres potencias son distintas, pero el número $6$ se puede escribir como un producto: $6=2\cdot 3$. Al hacer este cambio, ya tendremos algunas bases comunes:

SOLUCION

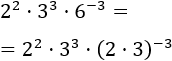
Aplicamos la propiedad de la potencia de un producto:

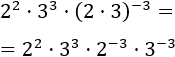
Ahora, sumamos los exponentes de las bases comunes:

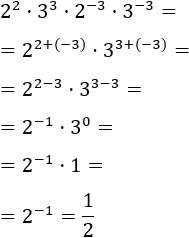
Ejercicio 5 

Calcular el cociente de productos de potencias:

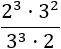
SOLUCION:

Como tenemos una división, restamos los exponentes del denominador a los exponentes del numerador con igual base:

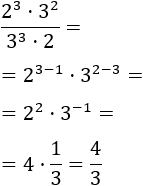
ACTIVIDAD EN CASA:

TRABAJA PAGINA 161