Ciencia Exactas: CLASE DE GEOMETRIA GRADO 11° DEL 15 DE OCTUBRE DEL 2025 SEMANA TEMA: LA HIPERBOLA

	ÁREA: GEOMETRIA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 15 DE OCTUBRE DEL 2025	PERIODO: CUARTO
	VALOR: LA AMISTAD	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 15 DE OCTUBRE DEL 2025

GRADO: 11°

TEMA: LA HIPERBOLA

SUBTEMA: EJERCICIOS PROPUESTOS

LOGRO. Identifica las secciones cónicas, las clasifica y realiza operaciones básicas aplicando la ecuación fundamental ellas.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué es la hipérbola?. lluvia de ideas.

LA HIPERBOLA:

¿Qué es una hipérbola?

La hipérbola es una curva abierta de dos ramas, cuya definición matemática es la siguiente:

En geometría analítica, una hipérbola es el lugar geométrico de los puntos del plano que cumplen la siguiente condición: el valor absoluto de la diferencia de las distancias desde un punto cualquiera de la hipérbola hasta dos puntos fijos (llamados focos) debe ser constante.

Además, el valor de la resta de esas dos distancias siempre es equivalente a la distancia entre los dos vértices de la hipérbola.

$\lvert d_1 - d_2 \rvert = 2a$

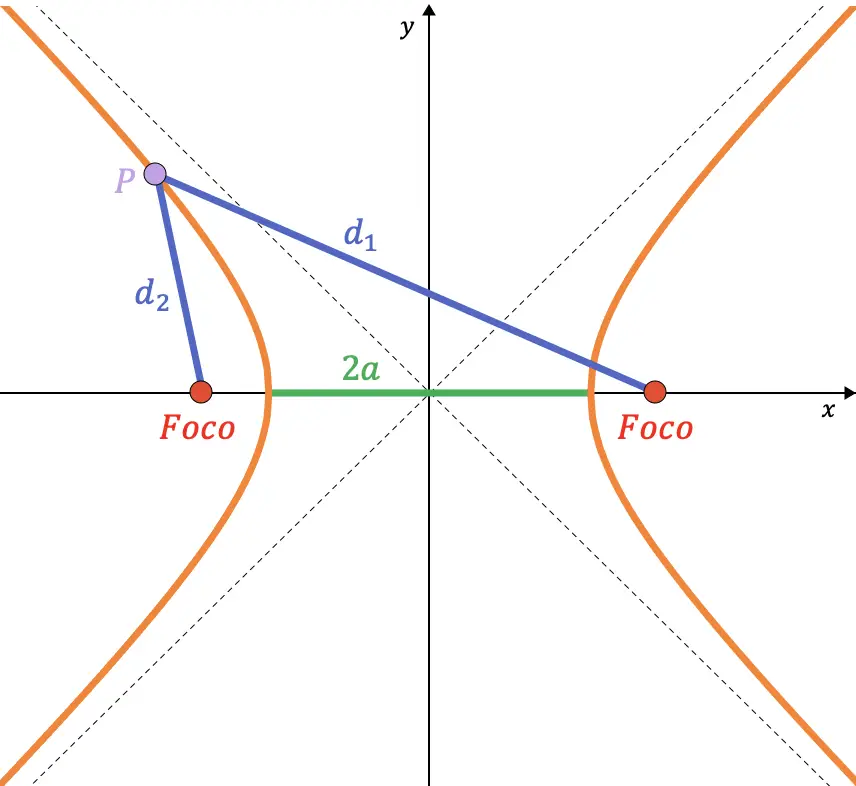
Más abajo veremos qué significa el coeficiente $a$ de una hipérbola.

ECUACION DE LA HIPERBOLA:

La fórmula de la ecuación ordinaria de la hipérbola en coordenadas cartesianas es la siguiente:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Donde:

$x_0$ y $y_0$ son las coordenadas del centro de la hipérbola: $O(x_0,y_0)$
$a$ es la longitud del semieje mayor de la hipérbola.
$b$ es la longitud del semieje menor de la hipérbola.

Ejercicios resueltos de hipérbolas

Ejercicio 2

Halla las coordenadas del centro, los vértices, los focos, el valor de la excentricidad y las asíntotas de la hipérbola cuya ecuación viene definida por:

$\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1$

Para determinar las coordenadas de cada foco, debemos averiguar el valor de la semidistancia focal (parámetro $c$ ). Y, para ello, podemos usar la fórmula que relaciona los elementos de una hipérbola:

$c^2 = a^2+b^2$

$c = \sqrt{a^2+b^2}$

$c = \sqrt{5^2+12^2} = \sqrt{169} =13$

Por lo tanto, hay un espacio de 13 unidades entre el centro y los focos. Con lo que las coordenadas de cada foco son:

$\bm{F(-13,0) \qquad F'(13,0)}$

CALCULO DE LA EXCENTRICIDAD EERCICIO PROPUESTO EN LA CLASE ANTERIOR

Luego, para calcular la excentricidad de la hipérbola debemos utilizar su fórmula correspondiente:

$e= \cfrac{c}{a} = \cfrac{13}{5} = \bm{2,6}$

Y, por último, hallamos las asíntotas de la hipérbola con sus fórmulas:

$y= \cfrac{b}{a} x \ \longrightarrow \ \bm{y=}\mathbf{\cfrac{12}{5}}\bm{ x}$

$y= -\cfrac{b}{a}x \ \longrightarrow \ \bm{y=-}\mathbf{\cfrac{12}{5}}\bm{ x}$

Ejercicio 3

Calcula la ecuación de la hipérbola con centro en el origen de coordenadas sabiendo que la diferencia de distancias desde un punto de la hipérbola hasta los focos F(-4,0) y F(4,0) es de 6 unidades.

SOLUCION:

Primero de todo, como la hipérbola tiene el centro en el origen de coordenadas, utilizaremos la ecuación canónica o reducida:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

Luego, según la definición de hipérbola, el valor absoluto de la diferencia de distancias de cualquiera de sus puntos hasta los focos (que en este caso es 6) debe ser igual a la longitud del eje real ( $2a$ ). Por tanto:

$\lvert d_1 - d_2 \rvert = 2a$

$6 = 2a$

$\cfrac{6}{2} = a$

$3 = a$

Por otro lado, el centro de la hipérbola es el punto (0,0) y un foco el punto (4,0). De modo que la distancia en ambos puntos (parámetro $c$ ) son 4 unidades.

$c =4$

Ahora podemos averiguar el valor del parámetro $b$ con la relación matemática que hay entre los 3 coeficientes característicos de la hipérbola:

$c^2 = a^2+b^2$

$b^2 = c^2-a^2$

$b = \sqrt{c^2-a^2}$

$b= \sqrt{4^2-3^2} = \sqrt{16-9} =\sqrt{7}$

Así que la ecuación de la hipérbola es:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

$\cfrac{x^2}{3^2}-\cfrac{y^2}{\left(\sqrt{7}\right)^2} = 1$

$\cfrac{\bm{x^2}}{\bm{9}}-\cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$

EJERCICIO 4

4) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

5 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

ACTIVIDAD EN CASA:

RESUELVE LOS SIGUIENTES EJERCICIOS

1. ¿Cuál es la ecuación de la hipérbola con centro en el punto (-3,4), una longitud del semieje real de 5 unidades y una longitud del semieje imaginario (paralelo al eje Y) de 12 unidades?

2. Halla las coordenadas del centro, los vértices, los focos, el valor de la excentricidad y las asíntotas de la hipérbola cuya ecuación viene definida por:

x^2/36-y^2/81=1

3. Calcula la ecuación de la hipérbola con centro en el origen de coordenadas sabiendo que la diferencia de distancias desde un punto de la hipérbola hasta los focos F(-7,0) y F(7,0) es de 10 unidades.

Ciencia Exactas

TALLER DE RECUPERACION 11° DE MATEMATICA IV P DEL 28-30 DE OCTUBRE DEL 2025 TEMA: LIMITES

miércoles, 15 de octubre de 2025

CLASE DE GEOMETRIA GRADO 11° DEL 15 DE OCTUBRE DEL 2025 SEMANA TEMA: LA HIPERBOLA

¿Qué es una hipérbola?

Ejercicios resueltos de hipérbolas

Ejercicio 2

Ejercicio 3

No hay comentarios.:

Publicar un comentario