CLASE DE MATEMATICA GRADO 10° DEL 14 DE OCTUBRE DEL 2025 SEMANA TEMA: TRIANGULOS NO RECTANGULOS

 

	ÁREA: MATEMATICA	GRADO: 10°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 14 DE OCTUBRE DEL 2025	PERIODO: CUARTO
	VALOR: LA  AMISTAD	FRASE:  “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION

FECHA: DEL 14 DE OCTUBRE DEL 2025

 GRADO: 10°

TEMA: TRIANGULOS NO RECTANGULOS   SUBTEMA: LEY DEL COLSENO

LOGRO. Reconoce el las funciones trigonométricas

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Que son los triángulos no rectángulo? lluvia de ideas. 

QUIZ.

DEFINICION PAGINA 179

LEY DEL COSENO

¿Que es la ley de cosenos?

Como se acaba de mencionar, la ley de cosenos permite hallar cuánto mide el lado de un triángulo no rectángulo, es decir, un triángulo oblicuángulo, e incluso los ángulos, no obstante, para ello se deben tener algunos datos en concreto. En primer lugar, para hallar el lado que se desconoce de un triángulo oblicuángulo necesitaremos saber cuánto miden los otros dos lados y el ángulo adyacente entre estos dos lados, es decir, el ángulo opuesto al lado desconocido.

Y si se desconocen todos los ángulos, será necesario conocer cuánto miden todos los lados, es decir, tener el valor de a, b y c. Se debe tener siempre presente que los ángulos estarán identificados con letras mayúsculas (A,B, C) mientras que los lados con letras minúsculas (a, b, c). La ley de coseno también es conocida como teorema del coseno y

Fórmula de la ley de cosenos

La ley de cosenos dice que en todo triángulo el cuadrado de un lado es igual a la suma entre los otros dos lados menos el doble producto de ellos multiplicado por el coseno del ángulo entre ellos. Las fórmulas para le ley de cosenos serían las siguientes:

En caso de tener el valor de cada uno de los lados del triángulo y se deban hallar los ángulos, se necesitará despejar el coseno, quedando la fórmula de la siguiente forma:

Ejemplos de la ley de cosenos

A continuación encontrarás algunos ejemplos en donde se resuelven ejercicios aplicando la ley o teorema del coseno.

Primer ejercicio:

En el siguiente ejemplo vemos un triángulo no rectángulo en el cual se desconoce su lado b y sus ángulos adyacentes, es decir A y C.

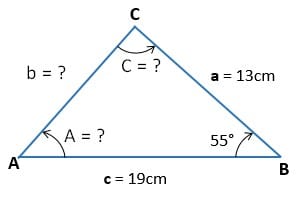
Primero se halla el lado b, para lo cual se realiza el siguiente procedimiento:

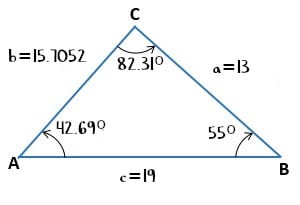
Posteriormente se calcula el ángulo A o C; en este caso se despejará A:

Conociendo el ángulo A y B es posible hallar el ángulo C del siguiente modo:

De este modo quedaría resuelto este primer ejercicio y tendríamos todos los valores del triángulo.

Segundo ejercicio:

En el siguiente ejercicio nos revelan el valor de todos los lados del triángulo, siendo necesario hallar todos los ángulos.

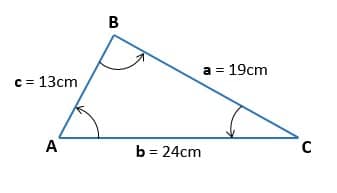
El primer ángulo que se hallará será A, para ello se aplicará una de las fórmulas vistas anteriormente.

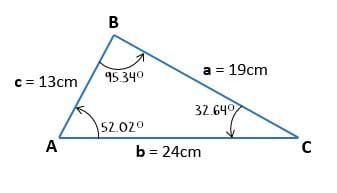
Tras hallar el ángulo A se procede a hallar el ángulo B y se usa la fórmula correspondiente para lograrlo.

Finalmente se halla el ángulo C con su respectiva fórmula.

Para comprobar que todos los ángulos son correctos se hace el siguiente procedimiento:

Y así comprobamos que el ejercicio lo hemos completado correctamente y tenemos el triángulo resuelto.

ACTIVIDAD EN CASA:

EJERCICIO 1

¿Cuál es la longitud del lado c si es que tenemos las longitudes a=6 y b=7 y el ángulo C=40°?

EJERCICIO 2

Si es que tenemos las longitudes b=10 y c=8 y el ángulo A=25°, ¿cuál es la longitud del lado a?