CLASE DE LOGICA Y ESTADISTICA GRADO 11° DEL 15 DE OCTUBRE DEL 2025 TEMA: MEDIDAS DE PESO Y MASA

 

	ÁREA:  LOGICA Y ESTADISTICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 15  DE  OCTUBRE DEL 2025	PERIODO: CUARTO
	VALOR: LA  AMISTAD	FRASE:    “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL  15 DE OCTUBRE DEL 2025

 GRADO: 11°

TEMA: COVERSION DE UNIDADES DE LONGITUD.

SUBTEMA:  TABLAS DE PREFIJO DEL SISTEMA INTERNACIONAL DE UNIDADES

LOGRO. Reconoce  las medidas de longitud las aplica en situaciones cotidianas

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué una medida de peso?. lluvia de ideas.

CONVERSION DE UNIDADES DE LONGITUD

LOGICA

Tabla de prefijos del Sistema Internacional de Unidades

Además de las equivalencias entre diferentes unidades de longitudes, la tabla de prefijos nos sacará de muchos apuros. Los prefijos nos permiten expresar cantidades muy grandes o muy pequeñas de una manera práctica.

Conversión de unidades

Para convertir unidades, vamos a revisar 2 métodos:

• Método de la regla de tres: este método es un clásico, lento pero seguro.
• Método del factor de conversión: el factor de conversión es una fracción, en la cual el numerador, es igual al denominador.

Veamos algunos ejemplos:

Ejemplo 1:

Convertir 3 metros (m) a pulgadas (in).

Solución usando regla de tres:

Usaremos la clásica regla de tres, teniendo en cuenta que 1 metro = 39,3701 pulgadas (in).

Solución usando un factor de conversión:

Con el método del factor de conversión, solo necesitamos saber que 1 metro = 39,3701 pulgadas (in).

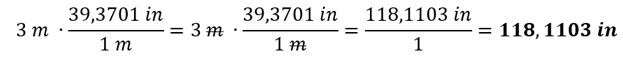
Ejemplo 2:

Convertir 2 pies (ft) a metros (m).

Solución:

Para convertir a metros, usaremos un factor de conversión, teniendo en cuenta que: 1 pie es igual a 0,3048 metros.

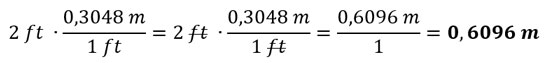
Ejemplo 3:

Convertir 4,5 millas (mi) a kilómetros (km)

Solución:

Para convertir a metros, usaremos un factor de conversión, teniendo en cuenta que: 1 milla (mi) es igual a 1,60934 kilómetros.

ACTIVIDAD EN CASA:

EJERCICIO 1. Convierta 6 km a pies

 EJERCICIO 2. Convierta 5 millas/h a m/s 

EJERCICIO 3. Convierta 96500 cm³/min a gal/s

EJERCICIO 4. Convierta 1.2 km a in "pulgadas"

ESTADIITICA:

DIAGRAMAS DE CAJAS:

DIAGRAMAS DE CAJAS Y BIGOTES

PROBLEMA DE CAJA Y BIGOTE.

En un bosque plantaron veinte (N=20) árboles y, al cabo de unos años, se mide la altura para ver su evolución. Un muy buen método para ver cómo han crecido y comprobar si existen valores extremos es el diagrama de caja. Mediante esta representación gráfica podemos ver si hay árboles que han crecido más o menos de lo habitual.

1. Se ordenan los datos
2. Se calculan los tres cuartiles.

3. 
   
   A partir del conjunto ordenado calculamos los cuartiles:

1. Los tres cuartiles son Q1=4,20, Q2=5,50 y Q3=6,42.

2. Se calculan los límites admisibles inferior y superior (LI y LS) para determinar los valores extremos.

3. 
   

4. 
   

   El rango intercuartílico es:

   
   
   

   A partir del rango calculamos los límites:

   

   
   
   
   

   
   
   

   Los valores extremos serán todos los árboles que midan menos de 0,96m o más de 9,59m. Tenemos dos árboles, uno de 0,94m y otro de 10,14m que serán valores extremos. Estos valores los representamos con puntos en el diagrama de caja.

5. El mínimo es el menor elemento del conjunto que sea mayor o igual al límite inferior. El máximo es el mayor elemento que sea menor o igual al límite superior. En este caso, el mínimo es 2,98 y el máximo 7,13.
6. Se dibujan los brazos del diagrama de caja. El brazo inferior irá desde el primer cuartil hasta el mínimo (desde el 4,20 a 2,98). El brazo superior abarcará desde el tercer cuartil hasta el máximo (desde el 6,42 hasta el 7,13).
7. Los dos puntos extremos se representan mediante un punto o círculo.

El diagrama de caja del conjunto de la altura de estos veinte árboles es:

Esta representación proporciona una visión rápida de la distribución, apreciándose una asimetría al no estar Q2 en el centro, en este caso porque hay árboles más altos que la mediana cuya altura está más separada de la mediana que los que tienen una altura inferior a ella, que están más agrupados. También se puede apreciar la existencia de valores extremos.

Ejercicios del Diagrama de cajas y Bigotes

a) Se realizó una encuesta colectiva de edades de un grupo de personas que asisten a un restaurant X

36

25

37

24

39

20

36

45

31

31

39

24

29

23

41

40

33

24

24

40