CLASE DE MATEMATICA GRADO 11° DEL 12 DE MARZO DEL 2025 SEMANA # TEMA: EL VALOR ABSOLUTO

 

	ÁREA: MATEMATICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL  12 DE MARZO DEL 2025	PERIODO: PRIMERO
	VALOR: SENTIDO DE PERTENENCIA	FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

         

FECHA: DEL  12  DE MARZO DEL 2025

 GRADO: 11°

TEMA: EL VALOR ABSOLUTO      

SUBTEMA: VALOR ABSOLUTO

LOGRO. Reconoce el conjunto de las desigualdades de los números reales.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Que es valor absoluto?. lluvia de ideas.

VALOR ABSOLUTO

DEFINICION PAGINA 43 DEL LIBRO

   

VALOR ABSOLUTO

¿Qué es el valor absoluto?

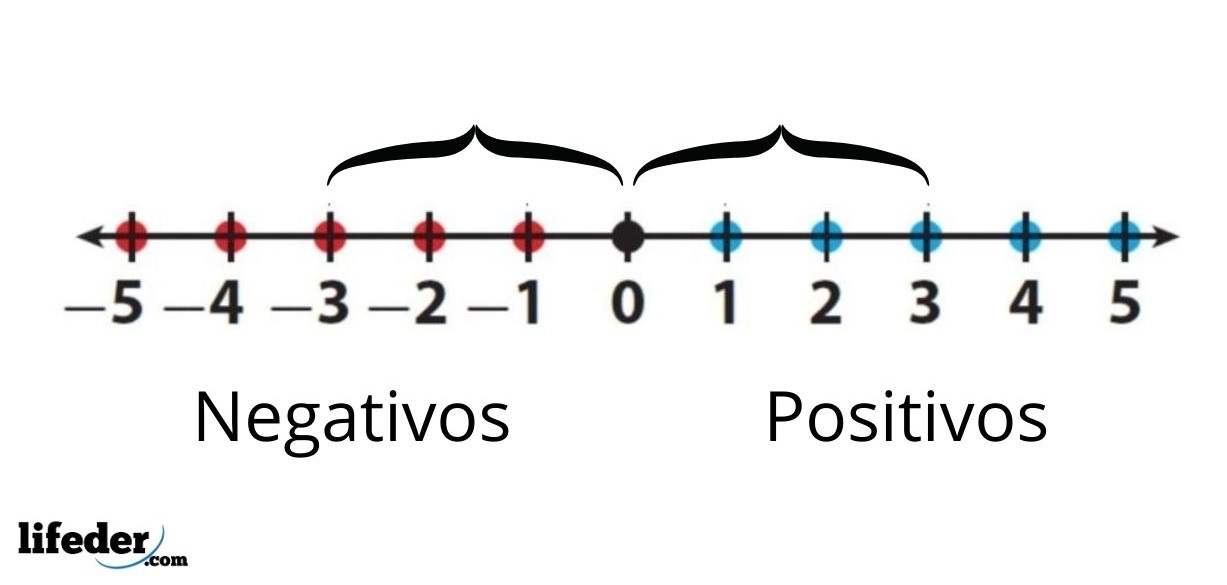
El valor absoluto de un número real se define como la distancia que hay entre ese número y el 0 de la recta real. Por ser una distancia, su valor es siempre positivo o cero e igual a la figura del número.

El valor absoluto se representa ubicando el número entre dos barras verticales, símbolo que se lee: “valor absoluto de”, tal como se resume en el siguiente cuadro:

Por ejemplo, el valor absoluto de -3 se escribe como │-3│ y es igual a 3. Esto significa que entre el -3 y el 0 hay tres unidades, que representa los números sobre la recta real. Por su parte el valor absoluto de +3 o simplemente 3, también es igual a 3, ya que al medir su distancia al 0 también es de tres unidades.

Ejercicio 1

Evaluar las siguientes expresiones algebraicas con valor absoluto:

a) │2x−5│ + │−x+1│  en x = 3

b) │(x−5)÷(x+4)│ en x = −1

Solución a

│2⋅3−5│ + │−3+1│=│6−5│ + │−2│=│1│+2 = 3

Solución b

│(−1−5)÷(−1+4)│= │(−6)÷(3)│=│−2│=2

ACTIVIDAD EN CASA:

1. REALIZA LOS SIGUIENTES EJERCICIOS

2. REALIZA PAGINA  45