ÁREA: GEOMETRIA | GRADO: 10° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 17 DE JULIO DEL 2025 | PERIODO: TERCERO | |
VALOR: SENTIDO DE PERTENENCIA | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 17 DE JULIO DEL 2025
GRADO: 10°
TEMA: ECUACIN DE LA CIRCUNFERENCIA
SUBTEMA: ECUACIN DE LA CIRCUNFERENCIA
LOGRO. Reconoce la diferencia entre los lugares geométricos
Ecuación ordinaria de la circunferencia
Antes de ver cuál es la ecuación de la circunferencia, vamos a recordar el concepto de circunferencia:
La circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.
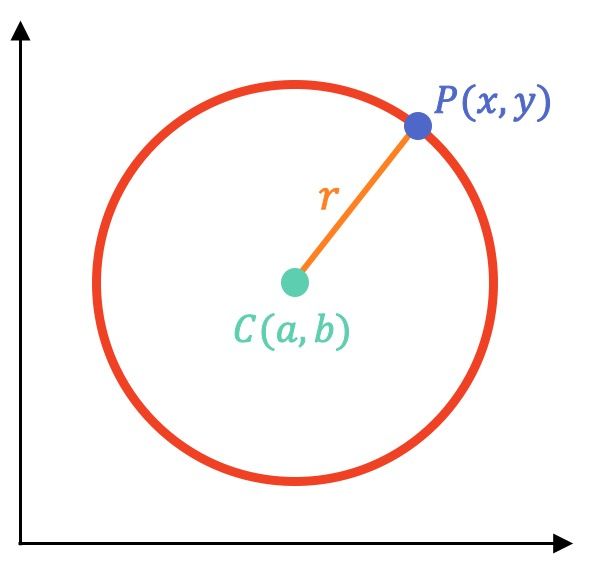
Por tanto, todos los puntos de una circunferencia están a una misma distancia de su centro.
Además, la circunferencia es una de las cuatro secciones cónicas junto con la elipse, la parábola y la hipérbola. Es decir, se puede obtener una circunferencia cortando un cono con un plano paralelo a su base.
La manera más fácil de describir una circunferencia en el plano cartesiano es a partir de su ecuación ordinaria. Así pues, la fórmula de la ecuación ordinaria de la circunferencia es la siguiente:
La ecuación ordinaria de la circunferencia es:
Donde:
es el radio de la circunferencia.
y
son las coordenadas del centro de la circunferencia:
Aunque no haremos la demostración porque es un poco tediosa, esta ecuación se puede obtener a partir del teorema de Pitágoras.
Veamos cómo se calcula la ecuación ordinaria de una circunferencia con un ejemplo:
- Determina la ecuación ordinaria de la circunferencia de radio 5 cuyo centro es el punto
La fórmula de la ecuación ordinaria de una circunferencia es:
ACTIVIDAD EN CASA:
INVESTIGAR BINOMIO DE LA DIFERENCIA DE CUADRADO


No hay comentarios.:
Publicar un comentario