ÁREA: MATEMATICA | GRADO: 8° | |
DOCENTE: ENAIDO MALDONADO POLO | CORREO: matematica. ceqa@gmail.com | |
FECHA: DEL 17 DE JULIO DEL 2025 | PERIODO: TERCERO | |
VALOR: SENTIDO DE PERTENENCIA | FRASE: “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION” |
FECHA: DEL 17 DE JULIO DEL 2025
GRADO: 8°
TEMA: OPERACIONES ADITIVAS POLINOMIOS
SUBTEMA: MULTIPLICACION DE MONOMIOS POR POLINOMIOS
LOGRO. Reconoce el valor numérico de un polinomio
ACTIVIDAD PREVIA: ¿Que es un polinomio?MULTIPLICACION DE MONOMIOS POR POLINOMIO
Solución:
Solución:
9.53 Multiplica (a+b+c)(a+b-c)
Solución:
Ten en cuenta: 1) Guarda el orden alfabético de la parte literal
después de calcular el producto
2) Coloca los términos semejantes en la misma
columna y si no coinciden escribe el término calculado más a la derecha.
Solución:
Solución:
9.53 Multiplica (a+b+c)(a+b-c)
Solución:
Ten en cuenta: 1) Guarda el orden alfabético de la parte literal
después de calcular el producto
2) Coloca los términos semejantes en la misma
columna y si no coinciden escribe el término calculado más a la derecha.
La multiplicación de monomios por polinomios consiste en multiplicar el término del monomio por cada uno de los términos que contiene el polinomio.- Multiplicar 2a por (b + a2), en este caso lo que se tiene es (2a)(b + a2), se tiene una multiplicación de 2a por el primer término del polinomio que es “b” y otra multiplicación de 2a por el segundo término que es “a2", por lo tanto se tendría:
(2a)(b + a2) = (2a)(b) + (2a)(a2) = 2ab + 2a3 Con la práctica se puede hacer la multiplicación de forma directa sin tener que hacer una separación de los términos, para quienes inician se recomienda hacer la separación para verificar el resultado. - Multiplicar 4b por (a2 – 3ab + 5b2c), otra forma recomendable para analizar es realizando la multiplicación en forma de columna. (a2 – 3ab + 5b2c)x (4b)4a2b – 12 ab2 + 20b3c
- Multiplicar 2a por (b + a2), en este caso lo que se tiene es (2a)(b + a2), se tiene una multiplicación de 2a por el primer término del polinomio que es “b” y otra multiplicación de 2a por el segundo término que es “a2", por lo tanto se tendría:
(2a)(b + a2) = (2a)(b) + (2a)(a2) = 2ab + 2a3 Con la práctica se puede hacer la multiplicación de forma directa sin tener que hacer una separación de los términos, para quienes inician se recomienda hacer la separación para verificar el resultado. - Multiplicar 4b por (a2 – 3ab + 5b2c), otra forma recomendable para analizar es realizando la multiplicación en forma de columna.(a2 – 3ab + 5b2c)x (4b)4a2b – 12 ab2 + 20b3c
Multiplicación de polinomios por polinomios
Se recomienda acomodar en forma de columnas, se multiplican los términos del multiplicando por cada uno de los términos del multiplicador, teniendo en consideración “la ley de los signos”, y el acomodo de los términos semejantes.
- Multiplicar (a + 3) por (3 – a): (a + 3)x (3 - a)– a2 – 3a + 3a + 9– a2 + 0 + 9El resultado de (a + 3)(3 – a) es –a2 + 9 que es lo mismo 9 – a2.
- Multiplicar (5 + 3a + 2a2 + 4b) por (5a + b): (5 + 3a + 2a2 + 4b)x (5a + b)5b + 3ab + 2a2b + 4b2 +20ab + 10a3 + 15a2 +25a5b + 23ab + 2a2b + 4b2 + 10a3 + 15a2 + 25aDe esta manera es más simple simplificar los términos semejantes.
ACTIVIDAD EN CASA:
Se recomienda acomodar en forma de columnas, se multiplican los términos del multiplicando por cada uno de los términos del multiplicador, teniendo en consideración “la ley de los signos”, y el acomodo de los términos semejantes.
- Multiplicar (a + 3) por (3 – a):El resultado de (a + 3)(3 – a) es –a2 + 9 que es lo mismo 9 – a2.(a + 3)x (3 - a)– a2 – 3a + 3a + 9– a2 + 0 + 9
- Multiplicar (5 + 3a + 2a2 + 4b) por (5a + b):De esta manera es más simple simplificar los términos semejantes.(5 + 3a + 2a2 + 4b)x (5a + b)5b + 3ab + 2a2b + 4b2 +20ab + 10a3 + 15a2 +25a5b + 23ab + 2a2b + 4b2 + 10a3 + 15a2 + 25a



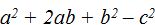
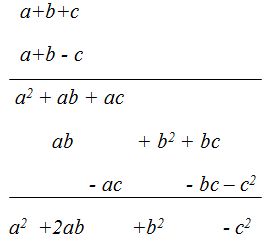

No hay comentarios.:
Publicar un comentario