CLASE DE MATEMATICA GRADO 10° DEL 15 DE JULIO DEL 2025 SEMANA TEMA: RAZONES TRIGONOMETRICAS

 

	ÁREA: MATEMATICA	GRADO: 10°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 15 DE JULIO DEL 2025	PERIODO: TERCERO
	VALOR: SENTIDO DE PERTENENCIA	FRASE:  “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL 15 DE JULIO DEL 2025

 GRADO: 10°

TEMA: FUNCIONES TRIGONOMETRICAS

SUBTEMA: FUNCIONES TRIGONOMETRICAS

LOGRO. Reconoce el las funciones trigonométricas.

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Que son ángulos coterminales? lluvia de ideas. 

RAZONES TRIGONOMETRICAS.

Las razones trigonométricas son relaciones entre los lados de un triángulo rectángulo que determinan sus ángulos. Este concepto está relacionado con operaciones matemáticas como el seno, coseno y tangente.

Los lados de un triángulo rectángulo están compuestos por dos catetos, o lados, y una hipotenusa. A su vez, los ángulos que describen este triángulo suman 180º en total, siendo uno de ellos 90º (llamado ángulo recto). Los otros dos ángulos son agudos, o sea menores de 90º, y podemos calcularlos a partir de las razones trigonométricas.

Las 6 razones trigonométricas y sus fórmulas

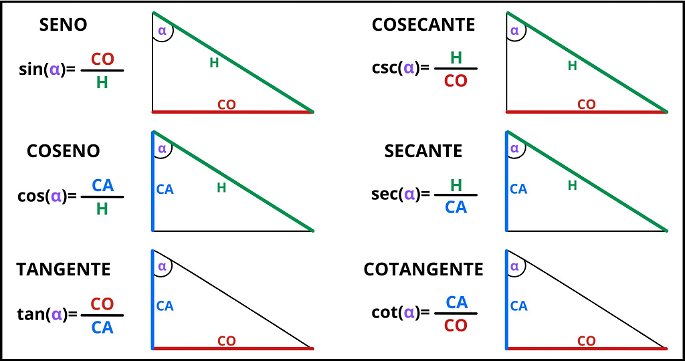
Las seis razones trigonométricas en un triángulo rectángulo son: seno, coseno, tangente, secante, cosecante y cotangente. Veamos una por una cómo se calculan estas razones y qué relación hay entre ellas, tomando como referencia un ángulo alfa (α).

EJERCICIOS.

Ejemplo

Por ejemplo, calculemos las razones trigonométricas del ángulo θ en los siguientes triángulos:

Figura 2. Dos triángulos semejantes tienen las mismas razones trigonométricas de sus ángulos. Fuente: Stewart, J.Precálculo: Matemáticas para el Cálculo.

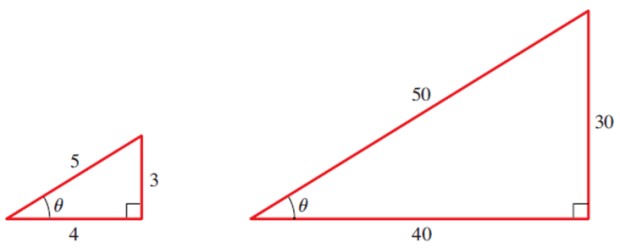
Para el triángulo pequeño tenemos las tres razones básicas del ángulo θ:

sen θ = 3/5

cos θ = 4/5

tg θ = ¾

Y ahora calculemos las tres razones básicas de θ con el triángulo grande:

sen θ = 30/50 =3/5

cos θ = 40/50 = 4/5

tg θ = 30/40 = ¾

Un detalle importante a tener en cuenta es el siguiente: tanto sen θ como cos θ son menores que 1, ya que los catetos siempre miden menos que la hipotenusa. En efecto:

sen θ = 3/5 = 0.6

cos θ = 4/5 = 0.8

Ejercicio 1

Calcular las razones trigonométricas de los ángulos mostrados en los siguientes triángulos:

 

Figura 3.- Triángulos para el ejercicio resuelto 1. Fuente: Carena, M. 2019. Manual de Matemática Preuniversitaria.

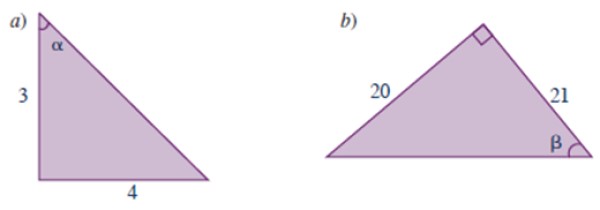
Solución a

Este triángulo es el mismo de la figura 3, pero nos piden las razones trigonométricas del otro ángulo agudo, denotado α. El enunciado no ofrece el valor de la hipotenusa, sin embargo, por aplicación del teorema de Pitágoras sabemos que vale 5.

Las razones se pueden calcular directamente de la definición, teniendo cuidado al seleccionar el cateto que sea el opuesto al ángulo α para calcular el sen α. Veamos:

• sen α = 4/5
• cos α = 3/5
• tg α = 4/3
• cot α = ¾
• sec α = 1 / (3/5) = 5/3
• cosec α = 1 / (4/5) = 5/4

Y como podemos ver, los valores de las razones trigonométricas se han intercambiado. En efecto, α y θ son ángulos complementarios, lo cual significa que suman 90º. En este caso se cumple que sen α = cos θ y así sucesivamente para las demás razones.

Solución b

Calculemos la hipotenusa del triángulo mediante el teorema de Pitágoras:

Hipotenusa2 = 202 + 212 = 841

√841 = 29

Entonces las 6 razones trigonométricas del ángulo β son:

• sen β = 20/29
• cos β = 21/29
• tg β = 20/21
• cot β = 21/20
• sec β = 1 / (21/29) = 29/21
• cosec β = 1 / (20/29) = 20/29

ACTIVIDAD EN CASA: DADOS LOS TRIANGULOS CON LADOS 3 Y4 COMO CATETOS HALLAR LA HIPOTENUSA Y LAS SEIS RAZONES TRIGONOMETRICAS Y EL TRIANGULO CON CATETOS 20 Y 21 REALIZAR LO MISMO DEL PRIMER TRIANGULO