CLASE DE LOGICA Y ESTADISTICA GRADO 11° DEL 24 DE SEPTIEMBRE DEL 2025 TEMA: MEDIDAS DE PESO

 

	ÁREA:  LOGICA Y ESTADISTICA	GRADO: 11°
	DOCENTE: ENAIDO MALDONADO POLO	CORREO: matematica. ceqa@gmail.com
	FECHA: DEL 24  DE  SEPTIEMBRE DEL 2025	PERIODO: CUARTO
	VALOR: LA  AMISTAD	FRASE:    “SOMOS CEQUEAMISTAS FORMADOS EN VALOR, LLEVAMOS EN LA SANGRE RESPETO-EDUCACION”

FECHA: DEL  24 DE SEPTIEMBRE DEL 2025

 GRADO: 11°

TEMA:  MEDIDAS DE PESO

SUBTEMA:  MEDIDAS DE PESO

LOGRO. Reconoce  las medidas de peso y masa y las aplica en situaciones cotidianas

ACTIVIDAD PREVIA: Exploro mis conocimientos. ¿Qué una medida de peso?. lluvia de ideas.

LOGICA

MEDIDAS DE PESO Y MASA:

Medidas de Peso

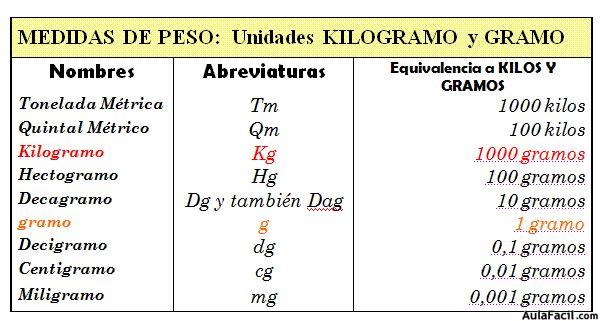
En las medidas de peso podemos utilizar el kilogramo y el gramo como unidades. También podemos considerar al gramo como un submúltiplo del kilogramo (1000 gramos).

Para pasar de una unidad superior a la siguiente inferior multiplicamos por 10.

Para pasar de una unidad inferior a la siguiente superior, dividimos por 10.

En el cuadro de las unidades introducimos 2 medidas de mucho uso como son la Tonelada Métrica y el Quintal métrico, ambos toman como unidad al Kilogramo.

7.31 ¿Cuántos gramos son 0,5 mg?
Respuesta:   0,0005 g
7.32 ¿Cuántos kilogramos son 12,5 cg?
Respuesta:  0,000125 Kg

7.33 ¿Cuántos gramos son 4 Qm?
Respuesta:   100000 g

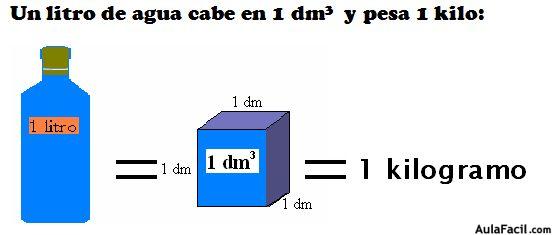
Relación entre capacidad, volumen y peso:

 

7.31 Un camión pesa 10 Tm vacío. Transporta un recipiente  de 30 m3  y está lleno de agua. Si el recipiente vacío pesa 2 Tm ¿cuántos kilos mueve el motor?
Respuesta:  42000 Kg

Solución:
Peso del camión vacío……………. 10000 Kg
Volumen de agua: 30000 dm3
Peso del agua……………………... 30000 Kg
Peso del recipiente vacío………….   2000 Kg
                                    Peso total…. 42000 Kg           

7.32 Calcula los 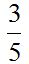 de 45 metros y exprésalos en centímetros.
Respuesta:   2700 cm

7.33 Calcula en dm la diferencia de las longitudes de dos alambres: 
Primer alambre mide 6 Dm, 8 dm:
Segundo alambre mide 3 m, 9 cm
Respuesta:    577,1 dm

7.34 Multiplica 4 Ha y 12 áreas por 8 y el resultado lo expresas en metros cuadrados:

Respuesta:  329600 m2

Solución:
  4 Ha equivalen a  4x10000 = 40000 m2
12 áreas equivalen a 12x100 =   1200 m2 
                          Total………     41200 m2
A este valor multiplicamos por 8 que es lo que nos pide el problema: 41200x8 = 329600 m2

ACTIVIDAD EN CASA:

1.  Multiplica 4 Dm, 3 m  y  6 dm  por   4m  y  8 dm.

Toda expresarlo a dm^2

ESTADIITICA:

MEDIA O VALOR ESPERADO

PROBLEMAS  DE MEDIA O VALOR ESPERADO

Continuación clase anterior

EJERCICIO 2. Dada una variable aleatoria definida en el intervalo [2,3] con función de densidad

  obtener media y varianza.

     

 

                  la varianza sería     o bien 

 

así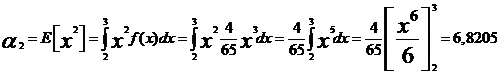   

                     luego la varianza será       

3. Una máquina fabricó placas de titanio para el Guggenheim  a un coste  de  1000 euros cada una . Las fabricaba con una holgura al alza entre 0 y 8 cm .Siendo la holgura una variable aleatoria . La holgura de la pieza ( siempre a mayor) no podía sobrepasar los 6 cm. ,las placas con mayor holgura no se podía utilizar y por tanto vender, pero si tenían un valor residual de 500 euros. Las placas útiles se vendían a 1500 cada una . Si para revestir la obra de Gerhy se fabricaron 20000 placas, calcular el beneficio esperado de la empresa que fabricó el revestimiento, conociendo que la holgura tenía una función de densidad f(x)=x/32.

 

función de beneficio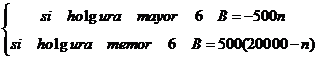      

PD = número de piezas desperdiciadas de una , variable aleatoria

PD = 0 es que la holgura es menor que 6

PD =1 es que la holgura es mayor que 6

                                       E[PD] = 0·P(x<6)+1·P(x>6)=0,437

                     P(x>6)=P(holgura mayor que 6)=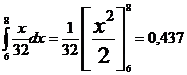

 

                         n = número de piezas desperdiciadas de 20000= 20000·PD

                       E[B]= -500E[n]+500(20000-E[n])

                       E[n]= 20000· E[PD]=8740

 

                                  Luego E[B] = -4370000+5630000=1260000 euros

 

4. Nuestra empresa produce miles de metros de tela al año . Tenemos un coste fijo para dicha producción de 10000 euros  .El coste de producción es de 10 euros el metro .

Si esperamos obtener unos beneficios de 3000 euros . ¿ A qué precio el metro tendremos que vender nuestra tela? ( la producción es una v.a. cuya función de densidad es )( se vende toda la producción)

 

                                  B=I-G   por lo que B= (X·1000·P)- (X·1000·10)-10000

 

Por lo que E[B]=3000=  1000P·E[X] -10000·E[X]-10000

 

                            E[X] =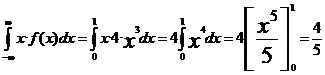 

Luego  E[B]= 1000·4/5 ·P-10000·4/5-10000 =3000  de donde  P =26,25 euros

ACTIVIDAD EN CASA:

EJERCICIO 1 Dada una variable aleatoria definida para los valores X={4,5} siendo su función de cuantía  P(x)=0,6x  .Obtener la media y el momento ordinario de orden dos, así como la varianza.

ACTIVIDAD EN CASA:

EJERCICIO 1 Dada una variable aleatoria definida para los valores X={4,5} siendo su función de cuantía  P(x)=0,6x  .Obtener la media y el momento ordinario de orden dos, así como la varianza.